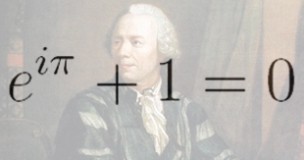Can maths be beautiful? Most people understand the beauty of a painting or a piece of music, but what about the squiggles of a mathematical equation? We call great works of art “beautiful” if they are aesthetically pleasing or express fundamental ideas in a profound way, and mathematicians feel the same way about particularly elegant proofs. Many say the most beautiful result of all is Euler’s equation: + 1 = 0. Leonhard Euler (pronounced “oiler”) was a Swiss mathematician in the 18th century, and is considered to be one of the greatest of all time. But to discover the beauty of Euler’s equation, you have to understand its meaning.
Irrational and imaginary
Let’s start with the numbers. You should be familiar with from your maths lessons at school. Divide the circumference of a circle by its diameter and the answer will always be 3.14159…, a decimal number that trails on forever. Numbers like
are called “irrational” because they can’t be written as a ratio or fraction.
The number e is also one you might have met at school. It crops up in many different areas of maths, science, and business, because the function f(x) = ex has the useful property of being its own derivative. In other words,
f'(x) = f(x) = ex.
This comes in handy for modelling processes like radioactive decay or interest payments, where the rate of change is proportional to the value you start with. Like , e is an irrational number that begins 2.71828… and goes on forever.
Numbers that never end are pretty strange, but i is even weirder. Multiplies of i are called “imaginary numbers”, but they’re no less real than the “ordinary” numbers. Mathematicians first used them to solve a problem with square roots, but they crop up in everything from electrical engineering to computer graphics.
To understand why we need imaginary numbers, work out the square root of 4. The obvious answer is 2, but -2 is also a root of 4 because multiplying two negative numbers gives a positive. But what’s the square root of -4? It can’t be 2 or -2, because squaring both of these gives 4. To solve the problem, we define the square root of -1 as i, so i2 = -1. This makes the square root of -4 equal to 2i, the square root of -9 equal to 3i, and so on. A number with both “real” and “imaginary” parts is called a complex number, and written as
a + bi.
By now you might be wondering what any of this has to do with “beauty”. These numbers are clearly useful, but it’s their combination that makes them beautiful. Rearranging Euler’s equation, we get . It seems almost impossible that these three strange numbers can unite to produce such a simple result – what does it even mean to raise e to the power of
?
Euler’s explanation
We know that a calculation like 23 can be written as 2 × 2 × 2, but isn’t as simple. Euler realised he needed a new method of exponentiation to handle complex numbers, and turned to the infinite for help.
The Taylor series of function turns a simple f(x) into an infinite sum. Any function that satisfies certain conditions can be expressed as a Taylor series, including ![]() :
:
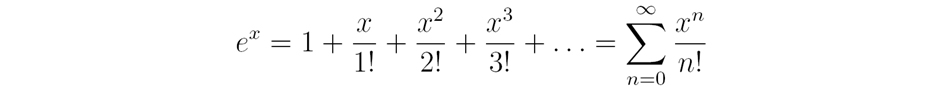
Here n! means “n factorial”, and n! = n × (n-1) × (n-2) × … 2 × 1. If you don’t believe this infinite sum adds up to ex, try putting x = 1. You can work out each term on a calculator, and you’ll find that the more terms you add, the closer the result is to 2.71828…
Euler realised that he could use the same formula for eix to get a similar result. Powers of i follow a certain pattern: i1 = i, i2 = -1, i3 = -i, and i4 = 1. When you reach i5 the pattern repeats, because i5 = i1 × i4 = i. Using this pattern, we can write:
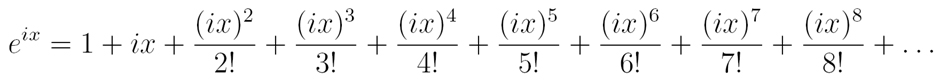
And by grouping real and imaginary parts we get:
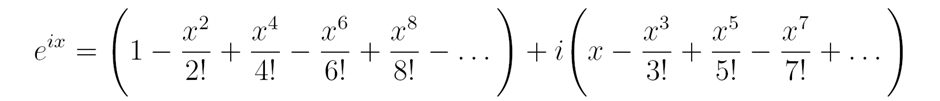
It turns out that the two groups form their own Taylor series. The first group is the Taylor series for cos(x), while the second group is the Taylor series for sin(x), which has been multiplied by i. This must mean that:
eix = cos(x) + i × sin(x).
We’ve cracked it. Now all that remains is to substitute :
= cos(
) + i × sin(
) = -1 + 0,
since cos() = -1 and sin(
) = 0.
So finally:
= -1
thus:
+ 1 = 0
Euler’s equation expresses a universal truth, valid in any language or culture. It contains five of the most important numbers in maths: 0, 1, e, i, and , along with the fundamental concepts of addition, multiplication, and exponentiation. These vital numbers and concepts also crop up in branches of science, engineering, and technology. All these ideas in just a few squiggles – if that’s not beautiful, what is?