Accountants do much more than just add up bills and work out taxes – some of them help solve crime. Financial fraud costs the UK over £30 billion a year, and many fraud cases involve falsifying records or hiding illicit transactions. Forensic accountants, the detectives in this criminal world of numbers, use their mathematical skills to hunt for clues and bring fraudsters to justice. One of their most useful sleuthing tools is a strange property of numbers known as Benford’s law.
Less is more
Benford’s law was actually first discovered in 1881 by an American astronomer named Simon Newcomb. While thumbing through a book of logarithms, he noticed that the front pages were more worn than the ones at the back. It seemed that people were looking up numbers beginning with 1 and 2 far more than those beginning with 8 and 9 – but why?
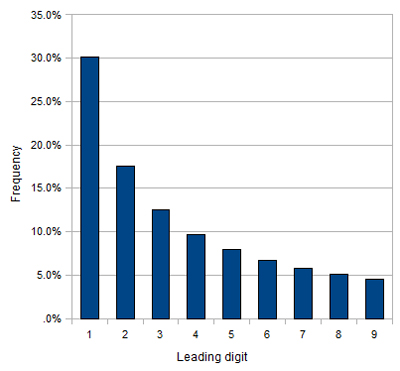
Intuitively, you’d expect numbers to follow a uniform distribution. There are nine possible leading digits, and none of them should be more likely than the rest, so each has one in nine or 11.1% chance of appearing. Newcomb theorised that this wasn’t true, and numbers beginning with lower digits naturally appeared in calculations more often than higher numbers. He produced a formula that said the probability of any random number beginning with d is log(1 + 1/d) for d = 1, 2,.., 9, so as the numbers go up, the probability goes down. Newcomb’s formula predicts that 30.1% of numbers begin with 1, while only 4.6% begin with 9. These percentages differ by a factor of more than 6, and that’s anything but uniform:
Unfortunately for Newcomb, no one took much interest in his strange fact about deteriorating logarithm tables and the formula was ignored. It lay dormant until 1938, when the physicist Frank Benford noticed the same effect in his own book of logarithms. To test the theory he collected over 20,000 numbers, anything from river sizes to sports statistics, and analysed their first digits. Although he wasn’t aware of Newcomb’s previous finding, Benford came to the same conclusion; the number 1 is far more likely to be a leading digit than any other. With a mass of empirical evidence to back him up, people started to pay attention and investigate the consequences of Benford’s law.
Dodgy digit dealings
It’s certainly interesting, but how does this strange numerical quirk help bring criminals to justice? Imagine a crooked office worker stealing money from his employer by creating fake invoices paid to a private account. A constant stream of £100 transactions might look suspicious, so he tries to make the bills more realistic by picking a variety of amounts: £43, £96, £17 and so on. These numbers look innocently random, but a forensic accountant’s analysis will quickly reveal they don’t follow Benford’s law, and something fishy must be going on.
Not all number sets follow Benford’s law though, and part of a forensic accountant’s skill is knowing when to apply the rules – if the numbers are artificially constrained in some way, it will skew their distribution. For example, a 99p shop is likely to have a high number of transactions beginning with a 9, but that doesn’t mean the shop assistants are cooking the books. Completely random numbers don’t fit either, as a tally of dice throws will list the numbers 1 through 6 with equal frequency of around 16.7%. Benford’s law covers sets of numbers somewhere in between the two extremes.
All in the mix
Recognising when to apply Benford’s law is one thing, but understanding why it works is another. Why is 1 so special when it comes to leading digits? One explanation is money in a bank account. Suppose you deposit £100 and start collecting interest. That leading 1 won’t roll over to a 2 until your savings have increased by 100%, but the jump from £200 to £300 only takes another 50% increase. From there its a 33% increase to reach £400, a 25% increase to reach £500, and so on. Each increase in the leading digit takes less time than the one before, so a list of bank balances is more likely to contain numbers starting with 1 than any other digit.
Not convinced? Another explanation of Benford’s law relies on the concept of scale invariance – the rule still applies even if you multiply the data by a scaling factor. In other words, bank balances follow Benford’s law no matter what currency you use, because converting from pounds to dollars preserves the distribution of leading digits. The table to the left illustrates a bank account paying 10% interest in pounds, and the same bank account converted in to dollars at an exchange rate of £1 = $2. As the numbers in bold show, the leading digit is a 1 in both currencies roughly 30% of the time.
|
£100.00 |
$200.00 |
|
£110.00 |
$220.00 |
|
£121.00 |
$242.00 |
|
£133.10 |
$266.20 |
|
£146.41 |
$292.82 |
|
£161.05 |
$322.10 |
|
£177.16 |
$354.31 |
|
£194.87 |
$389.74 |
|
£214.36 |
$428.72 |
|
£235.79 |
$471.59 |
|
£259.37 |
$518.75 |
|
£285.31 |
$570.62 |
|
£313.84 |
$627.69 |
|
£345.23 |
$690.45 |
|
£379.75 |
$759.50 |
|
£417.72 |
$835.45 |
|
£459.50 |
$918.99 |
|
£505.45 |
$1,010.89 |
|
£555.99 |
$1,111.98 |
|
£611.59 |
$1,223.18 |
|
£672.75 |
$1,345.50 |
|
£740.02 |
$1,480.05 |
|
£814.03 |
$1,628.05 |
|
£895.43 |
$1,790.86 |
|
£984.97 |
$1,969.95 |
These explanations makes sense when dealing with financial data, but Benford’s law applies to more than just money. In 1995, the American mathematician Ted Hill realised the key to Benford’s discovery was the breadth of his data. Hill proved that random samples drawn from random distributions will always converge to Benford’s log(1 + 1/d) distribution. For example, a newspaper might contain articles about share prices, environmental pollution, and political polls. The numbers in these articles are all samples from different distributions, but when taken together the familiar pattern of Benford emerges. What started as a few scuffed pages became a crime-fighting mathematical proof, helping forensic accountants catch crooks around the world.