50p coin
The British 50p coin, like the 20p coin, has a rather unusual shape. It is an equilaterally curved heptagon. That is, it has seven equal sides, all of which are curved. Like a circle, it has a fixed diameter, but clearly it isn’t as round as a circle. However, equally clearly, it is rounder than a regular heptagon, which has straight sides.
You might be tempted to ask: “So, just how round is it?” Does this question even make sense? Can we quantify roundness? As it happens, we can! So let’s see if we can determine just how round a 50p coin is.
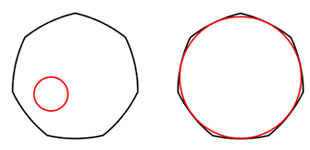 Notice that the MIC just touches the middle of the curved sections of the heptagon. |
Inner circle
Start by drawing a small circle somewhere inside the heptagon shape. Gradually make the circle bigger and move it about within the heptagon until it is as big as possible while remaining inside the heptagon (the circle may touch the heptagon, but may not cut through it). The resulting circle is called the maximum inscribed circle (MIC).
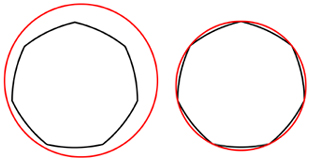 Here, the MCC just touches the vertices of the heptagon. |
Outer circle
Now draw a large circle surrounding the heptagon. Gradually make this circle smaller and move it about until it is as small as possible while remaining outside the heptagon (again, the circle may touch the heptagon, but may not cut through it). This circle is called the minimum circumscribed circle (MCC).
Roundness
The difference between the radius of the MCC and that of the MIC is defined to be the roundness. This definition is known as the minimum zone circle, or MZC, roundness. Other definitions are possible. For a perfect circle the MCC and MIC are the same as each other, so the roundness of a perfect circle is zero.
For our curved heptagon we can calculate the radius of the MCC to be
![]()
and that of the MIC to be
![]()
where d is the diameter of the curved heptagon and θ is the angle 2π/7 radians (or approximately 51.4°). For the 50p coin, the diameter, d, is 27.3mm, so rMCC and rMIC are approximately 14.0mm and 13.3mm respectively, giving a roundness of 0.7mm. Notice that roundness has dimensions of length.
What is the roundness of a 20p coin, whose diameter is 21.4mm? See if you can calculate the roundness of a regular heptagon (i.e. one with straight sides), or other regular polygons.
The symmetry of our 50p coin means that its maximum inscribed and minimum circumscribed circles both have the same centres. In general, for more asymmetric shapes, this won’t always be the case, but isn’t necessary for the definition of roundness to hold.
In most engineering situations you would probably have several discrete measurement points describing the shape of a component, rather than a continuous curve. As long as you can find a minimum circumscribing circle and a maximum inscribing circle for the points though, you can still estimate a value for the roundness of the component.
Who cares?
Why should we care about having a precise definition of roundness? Do we really need to know exactly how round a 50p coin is? Possibly not, but there are plenty of situations in science and engineering where it is important to have such a measure.
For example, a spinning shaft in a hydraulic pump or a gas turbine might experience dangerous vibrations if not sufficiently round. In 1986 the space shuttle Challenger exploded shortly after lift-off. The investigating committee decided there were three main factors contributing to the disaster: the O-ring seal, the booster joint and out-of roundness of the booster fuel containers.
It’s not just an academic exercise – lives may depend on knowing just how round something is! Mathematicians are involved not only in deciding how to define roundness, but also in improving the instruments used to measure roundness, and in improving and monitoring the processes used in manufacturing critical components.






