Make a real effort to do all the assignments and worksheets for every module you are taking in your study time and do them on time. It is pointless to wait for the answer handouts and then think “I could have done that!” because in real life or the exam you will not be able to. Note that exam questions are often similar to, and sometimes easier than, those on the problem sheets. If you fall behind with problem sheets, lectures will become (even more) mysterious and far less useful to you; think about planning better by consulting the Time Management section of this guide and get some help from your study advisers if the problem persists or gets worse. Don’t ignore it!
When you are doing a worksheet, FOCUS on it exclusively! No phone or television should be on to distract you. Don’t attempt to do an entire sheet of problems at one sitting! Instead set yourself a clear goal and time limit for doing problems e.g. problems 1-3 in 20 minutes. When 20 minutes is up, either finish them off if you are ‘on a roll’, or stop and write down what it is that you don’t follow. Take these questions to a seminar or tutorial … or even friends; only then you should go back to the problems that you haven’t tackled (again as a 20-minute blitz).
Seminars give you a chance to ask about problems you have already had, not to start problems from scratch. If you have tried the problems beforehand, the seminar leader’s explanations will be much more useful to you. Do not be afraid to show that you do not understand any topic, no matter how basic; none of your friends will know how to do it either and it gives the seminar leader a good starting point for explanations and discussion. Always challenge solutions/answers if you think they are wrong; they might be, but even if they are not, you will have learned why (and this will also help your teacher in explaining to others in the future).
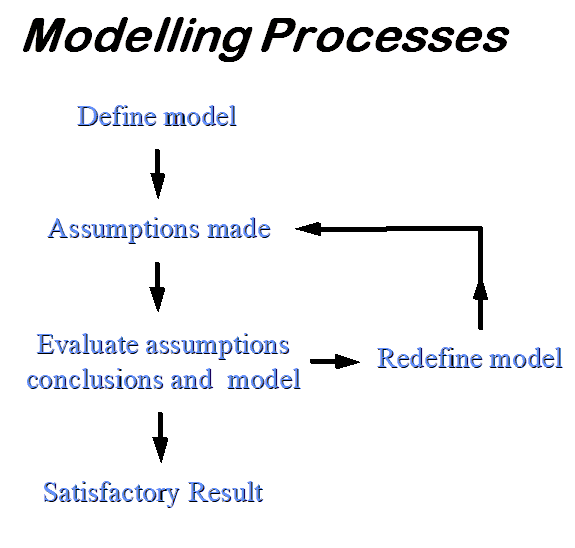
For many topics, a good solution will start with a fairly accurate diagram. Define the problem clearly. For complicated problems you may need several goes around a MODELLING CYCLE as follows: a) simplify the situation to produce a model, b) solve, c) interpret the results to see if they are sensible and adequate for your purposes: if so, stop, else d) refine the model, e) return to loop at b).
Does your solution contain some English sentences explaining clearly what you are doing and the strategy for achieving it? Refer to any theorems/results you use. Check your solution(s). I know it’s stating the obvious, but does your solution work? Substitute your values/solutions back into equations, differentiate indefinite integrals, check inverse matrices by evaluating AA-1, multiply out partial fractions, check boundary and initial conditions are satisfied for O.D.E.s, etc.
Is your answer dimensionally correct when expressed in terms of M(ass), L(ength) & T(ime), left in an exact form if possible e.g. ln(2) or if not exact, is it quoted to an appropriate level of accuracy (with an error estimate if possible) and in standard form using S.I. units (e.g. 3.2 x 105 ms-1)? Is it reasonable, both in terms of size and sign? For example, were you expecting the energy to be negative? If your answer is a formula, can you understand it in the limit of small or large x? Does the solution reflect the symmetry of the problem, if any?
For multi-choice questions, read and consider ALL the choices before deciding. If you can’t decide, make an informed guess (except in diagnostic tests of course!).
Before you get started with a problem, can you:
- specify precisely what the question is asking? Often this involves drawing a diagram, flow chart etc.
- define all the terms in formulae and equations and state their dimensions and units? If not, stop and get help.
- simplify the problem further before attempting a solution? For physical problems, non-dimensionalisation leaves only the important parameters, and so is often very useful. This depends on the nature of the problem and can often be hard, but is vital to your understanding of the true nature of the problem and well worth getting help with. Non-dimensionalisation can also dramatically help when seeking to write numerically stable programs and avoiding underflow/overflow problems.
- see any symmetry in the problem e.g. what happens if x -> -x or x and y are exchanged?
If you do get stuck, can you
- identify what mathematics is involved from your notes and books?
- make any estimates and see how sensitive the results are to your input assumptions?
- do sample calculations with numbers to see any sort of pattern?
- solve a simpler problem, perhaps by fixing one of the variables, or looking at what happens if z is real rather than complex?
- look at any sort of limiting case e.g. as x gets small or large in comparison to another parameter or variable?
- use a symbolic manipulator (e.g. Wolfram alpha or Geogebra) to solve the problem and then consider why the solution is as it is? (N.B. this is not a substiitute for doing the problem yourself!)
- plot a graph of the functions involved to see what’s going on? Pay attention to any special features like vertical asymptotes, turning points and large x behaviour.
- do the problem backwards from the answer to see what you can learn?
- get any help from your friends? Can you explain to them exactly what the problem is, and why you are getting stuck? This often results in a solution. If not and there is a group of you, you could start by “brainstorming” which involves writing down uncritically any idea anyone has for 5 minutes, and then examining these ideas for relevance and order of importance for the problem.
- If you still cannot do the problem, take a break, sleep on it or ask your lecturer. Remember that you will still have learned something in the attempts you have made and this will make you more receptive to the correct method or solution when you see it.
A useful and readable book is “How to solve it” G. Polya, Penguin.
Computing
Many assignments involve computing and/or word-processing. It will be a real advantage to you if you get your own PC or Mac and some final-year projects are not feasible without your own machine.
When programming make sure you really understand the structure of the problem and the flow of data before you attempt any actual coding. If you cannot draw an accurate flow diagram for the problem, stop and seek help. Do not attempt to start coding in the hope that something will become clear later – it will not – and any code you do write will be impossible to debug.
- Divide the problem into modules, write subroutines or external function subroutines for them and check each individually and thoroughly before linking into the main program. Always check each module with a problem you can solve analytically if this is at all possible e.g. for a root finding routine, will it give 1,-2 and 5 for the polynomial (x-1)(x+2)(x-5) or does the numerical integral of sin(x) work out before you attempt evaluation of functions you cannot integrate analytically? Always alter any numerical variables, such as number of iterations or integration range subdivision, to make sure your program works and your answers have converged.
- Is your code flexible? For example, can you easily alter the function to be integrated (leaving most of the program unaltered) and does it give the correct answer if the limits of integration are negative, or the top limit is less than the bottom limit?
- The main program should only control the data flow by calling these subroutines and should not contain any calculations. Check as above for subroutines.
- Write a subroutine for input; if input is to be from the screen, make sure the user knows what to input by writing statements to the screen such as “Input the number of iterations you require (an integer between 1 and 100)”. For complicated input, the chances of typing it all in correctly are slim, so read it from a previously-edited input file.
- Write a subroutine for output, with all the input data repeated first and clearly labelled, and then the results in a table with headers, or labels. If only a small amount of data is to be output, you can display this on the screen; large amounts of data should be written to a file (for later editing, printing or pasting into a report), but in interactive running, it is helpful to output some data to the screen so you know what is happening e.g. messages like “Starting iteration number …”.
- Use plenty of comments so that you and others can understand your program. Do this as you go along, not as an afterthought at the end.
- If your program gives unexpected results, write out most or all of the values of the variables to a file for inspection. This could be big, so don’t print it out and do only a few test cases/iterations; delete it afterwards.
Backup everything you do regularly on your University Network or to a cloud based service. If you use memory sticks be aware that they are easily lost!. Remember that PCs, especially notebooks PCs sometimes fail and regularly get stolen. Neither will be accepted as a valid excuse for non-submission.
Remember to use the spell-checker when word processing!. You should aim to write your essay directly onto the screen from your notes rather than writing it out in full beforehand. Get up early! Almost all university network PCs are free at 8 am and most are free at 9 am.
You might want/need to produce a Web page of your document, or put it on the Web for downloading. Here is a guide to creating a simple HTML page.
The temptation to download large quantities of material from Web sites etc. must be resisted. You will be discovered and get zero marks for it – or worse! Reference carefully any material, such as diagrams, you do use, including full Web site URL and date accessed if used.
Finally
Hand in your work on time, and to the correct place. Don’t wait until it is perfect … it never will be!
Great – you have handed in your work, got a good mark and read the feedback. End of story? Absolutely not; the task is not finished until you have ‘processed’ your feedback so that it feeds-forward into your next bit of work. Leave plenty of time for feedback and READ IT ALL when your work is returned to you. LEARN from your mistakes, rather than attempting to conceal them. If anything is not clear, ask your lecturer. If your mark is substantially lower than you expect, please ask your lecturer to explain where you lost marks and ask for suggestions for improving your work. N.B. This is not an invitation to try to negotiate your mark, which will not be changed, so don’t even try! Read the model solutions even if you have full marks already; there may be a better way of doing/expressing/presenting the solutions. Can you now identify where you lost marks? You might think that 60% is good, and so it is, but how could you have attained the other 40%? Ask if it isn’t clear (it usually is far from clear, especially for more discursive submissions). If you are in a study group, you can also benefit from reading other students’ submissions and the feedback they got as well. You might even go so far as to analyse why their mark was better/worse than yours to further understand how the marking criteria are applied.
Do not cheat in any way; it is very easy for your markers to spot work which is not your own and, in the case of copying from another student, both original and copied work may get zero marks, so don’t let others copy your work. If you do copy, any feedback you get will be of little benefit to you to improve your own understanding and writing style. Copying large sections out of a book, CD-ROM or Web site is equally pointless (whether you have referenced and/or edited the material or not) and will get you very low or zero marks. You need to read, digest and analyse the material, and then write it in your own words, preferably synthesised from several sources. There is no substitute for hard thinking about what you write, and copying everything down in the hope that some of it will be relevant will result in poor marks.
Quoting material from books or other sources without referencing them is plagiarism! This will normally result in you being awarded zero marks and disciplinary action being taken against you. If you are in doubt about what is acceptable and what is not, discuss it with the module lecturer, your tutor, your supervisor or the Undergraduate Course Director. You can learn more about understanding and, especially, avoiding ” unintended” plagiarism here
Look at these examples to see how (and how not!) to apply these rules in technical report writing, especially mathematics.
You should also look at E. Hunsicker, Plagiarism in Maths, Loughborough University course notes for MAC200 Mathematics Report, 2011 for more mathematically- advanced examples.
About the Study Skills pages
These pages were originally created by Martin Greenhow.

Study Skills by Martin Greenhow is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Study Skills – Time Management
Study Skills – Projects and Essays
Study Skills – Using Charts and Graphs
Study Skills – Postgraduate Research
Featured image by Jonathan Kemper on Unsplash






