We are always being told to keep our data safe, so why would anybody want to ban encryption?
One of the most important applications of mathematics in the last 100 years has undoubtedly been work related to encryption and code breaking. At the end of the Second World War Alan Turing’s team at Bletchley Park helped crack the Enigma Code and helped shorten the war by an estimated two years, with their work leading to the development of the first computers.
More recently with the invention of the internet, encryption has meant that we can communicate securely. Without encryption anyone would be able to easy steal your details and internet shopping just wouldn’t be possible.
In fact most of your time online would become pretty unsecure and difficult. When you transfer your bank details over the internet they are kept secret by what is called ‘public key cryptography’. (If you would like to read a mathematical explanation of public key cryptography take a look at this Nrich Article aimed at A-level students.)
At the heart of public key cryptography is the multiplication of prime numbers. It is very easy to multiply two numbers together (for example multiplying 83 X 71 is easy). If however you were given the number 5893 it would have taken you a while to factorise it and work out that 5893 = 83 X 71. In order to decrypt a message which has been encoded using public key cryptography you need to be able to factorise a given number quickly. If you can factorise the numbers then you can break the encryption. When the numbers used are larger it is much much harder to factorise them in a reasonable amount of time. In fact the difficulty of factorising numbers means that it is mathematically very tough to decipher messages which are encrypted using this method.
In the past there have been other methods of encryption which were thought to be unbreakable, so what is there to stop someone inventing an amazing algorithm which factorises large numbers very very quickly? The reason is that factorising numbers is a type of problem which mathematicians believe is fundamentally difficult, meaning that it is unlikely that large numbers will ever be factorised quick enough for messages to be decrypted efficiently. (Although mathematicians have still to prove this for certain!)
Did you know?
A semiprime is a number which is two prime numbers multiplied together. For example 35 is a semiprime becase 35 = 7 X 5. In 1991 RSA Laboratories published a list of semiprimes and offered cash prizes for their factorisation. The numbers have still not all been factorised, even to this day – showing just how difficult factorising semiprimes is. The largest number to be factorised in this challenge was 768 digits long and took two years and the equivalent of 2000 years of computing power!
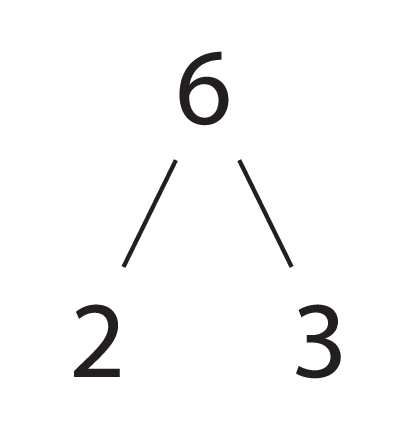
Six is a small example of a semiprime.
We are therefore at a stage in human history where we have invented encryption methods which our ancestors could only have dreamed of. So why are governments getting more worried about encryption if it is so useful and now so strong?
So far we have only talked about the benefits of encryption and how we can keep our messages and money safe from criminals. The flipside is that encryption can also benefit terrorists and criminals who want to communicate in private, preventing law enforcement agencies from intercepting their messages.
The reason that encryption is a hot topic again is that some messaging services such as Whatsapp have implemented what is known as ‘end to end encryption’. In the past when you sent a message your service provider had the key to unlock your messages.
The difference with services such as Whatsapp is that your message is only decrypted once it is on the phone of the person you are communicating with. In simple terms this means that even if Whatsapp HQ wanted to read your messages then they can’t.

This is when it becomes scary for governments who suddenly can’t access the communications of people who are suspected terrorists or criminals. There are however some other complicated ways of intercepting messages which use end to end encryption.
For example a user could be subject to what is known as a man-in-the-middle attack when someone impersonates the device of the person you are communicating with. Your phone could also be hacked and messages read once they are on your actual device rather than when they are in transit. We now have a difficult dilemma – ban or limit encryption which could lead to criminals accessing peoples’ communications or allow this strong type of encryption and make it easy for criminals to communicate secretly.
The whole issue of how much a government should be able to access people’s data is a massive political issue and is one of the places where maths meets politics. Whatever your view on people’s right to privacy, it is certain that the mathematics of encryption has changed the face of the modern world both for better and potentially also for worse.
If you are interested in a career in the field of cryptography then there are a number of places where you could work including in a university, private company or at GCHQ (Government Communications Headquarters). You should take a degree with a high mathematical content such as mathematics, statistics, physics or computer science. In the modern world there is going to be an ever increasing demand for clever, mathematically gifted people who can understand and work with technology.
If you are interested in a career as a mathematician at GCHQ then take a look at their website.
Article by Hazel Lewis
Main Image Credit: Yuri Samollov/Flickr by CC
Teaching ideas and resources to support the learning of topics covered in this article can be found on the National STEM Learning website









