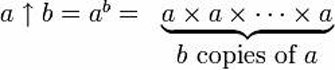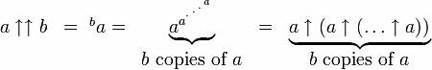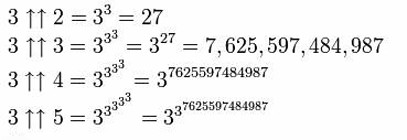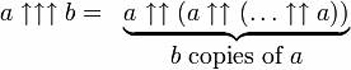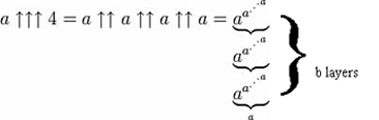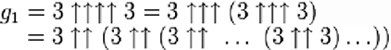Numbers go on forever – but on the way to infinity, there are some pretty remote way posts.
To our ancestors, a million was as big as numbers needed to get. There was no need to invoke the billions (1,000,000,000) of finance or the terabytes (1012) of computing. Technology has made us blasé about using 9 or 12 digit numbers in conversation. However, there’s a long way to go before we even catch up with the scale of our place in the universe, let alone the dizzyingly gigantic numbers mathematicians have dreamed up.
Standard numbers
Past a billion – the order of magnitude of the human population – we really have to wave goodbye to the idea of having names for numbers. (Although they do exist up to 1063, they’re not in common usage). For the distance light travels in a minute, the number of atoms in a gram of carbon, or the distance between galaxies, scientists use standard form to express themselves. Standard form records all numbers in the format a × 10n, where a is a number between 1 and 10 and n can be any number. It’s what you’d use to talk about the number of carbon atoms in a 12g sample. Which, incidentally, is 6.22 × 1023, Avogadro’s number, and quite large. The observable universe is about 8.8 × 1023 km wide, and there are an estimated 1087 particles in it. But bigger than those numbers by far are the constructs of mathematical minds.
Let me googol it for you
Immortalised in common usage by the internet giant, a googol is the number 10100 – 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. The American mathematician Edward Kasner asked his nephew Milton to name it, and a googol it became. But the next really big number is the googolplex, which raises 10 to the power of a googol. This is astronomically bigger than a googol – it’s impossible to write a googolplex down in standard notation even if you wrote a single digit on each particle in the universe.
The power of powers
Adding an exponential into the exponent really increases the rate of enlarging numbers.
3×3×3=27
3(33) = 7,625,597,484,987
Naturally, on a quest for bigger numbers, one would add more and more powers to the tower. This rapidly gets awkward to write down though, as well as resulting in towers that make Pisa’s look stable. Changing notation makes it possible to condense these towers down and express higher concepts.
Follow the arrows
Developing another way to denote powers:
Donald Knuth coined a new operator for repeated exponentiation (“tetration”), to bring those power towers down to earth.
In use, the double arrow looks like this:
This can be extended still further by adding a third arrow, creating the operation of ‘pentation’ – repeated tetration.
In words, that involves tetrating a to the a (so, a power tower of a ‘a’s), then building another tower of ‘a’s as high as that power tower, then using the result of that power tower to determine the number of ‘a’s in the next one –resulting in the calculating of b power towers, increasing in height according to the result of the previous tetration.
And more arrows can still be added, although thinking about the operations they denote may require more brain time than you’re prepared to devote to the issue. But armed with this notation, we can now acknowledge some truly big numbers.
Calling Ackermann and Graham
Mathematical proofs have given us some massive quantities. At the start of the twentieth century, mathematicians wanted to know how to tell if a sequence was computable – could a mechanical process for working it out be defined? It was proposed that a sequence was computable if it had the property of being ‘primitive recursive’. Wilhelm Ackermann threw a sequence-shaped spanner in the works by coining a sequence that, while computable, wasn’t primitive recursive. And it goes like this:
Start with the simplest mathematical operation possible – addition. Apply this to the first natural number, 1:
1 + 1 = 2
Then progress to the next operation, multiplication (repeated addition). Do this to the next number:
2 × 2 = 4
Next up is repeated multiplication – exponentiation to you and me – with 3 as a variable.
33 = 27
So far, so puny. But we just defined a function for repeated exponentiation, tetration, and if we do this to 4..
![]()
Looks small, has 10154 digits. And this is just the 4th term in the sequence.
Fifth is … a power tower of fives
digits high.
Sixth is . Just five symbols denote a number bigger than there is room for in the universe, even if you wrote each digit in a font 1nm wide. And the sequence continues.
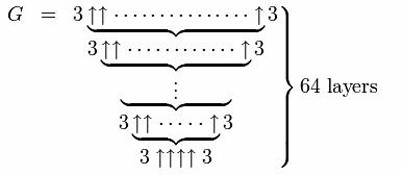
The same up-arrow notation was used by Ronald Graham to limit some properties of a hypercube (a cube in 4 spatial dimensions), although ‘Graham’s number’ is now better known simply for being collossal.
Graham’s number is defined like this:
The number of arrows in each layer is given by the result of evaluating the arrows in the layer below, until after 64 layers, the final number is reached. To give you some idea of the size of this, we can look at the first layer alone:
where the number of threess in the expression on the right is
Now each tetration () operation reduces to a “tower” of exponentiations (
) according to the definition
where there are X threes.
Thus,
where the number of threes is , becomes, solely in terms of repeated “exponentiation towers”, and where the number of threes in each tower, starting from the leftmost tower, is specified by the value of the next tower to the right.
That is, technically speaking, a lot of threes. Don’t relax yet though, as Graham’s number, while being the biggest number that mathematicians have yet needed to write down explicitly, is dwarfed by some products of computing theory. We don’t have space to go into them here, but check out ‘Who can write down the bigger number?’ by Scott Aaronson if Graham’s number just wasn’t enough for you. It also goes into more detail about the history of big numbers and their explanations.
Big, Bigger, Biggest
The world of numbers is, as you might expect, infinite. Nature is pretty big, but the numbers she requires us to use are far smaller than those that human mathematicians have dreamed up. In that sense, the human mind is bigger than the universe.