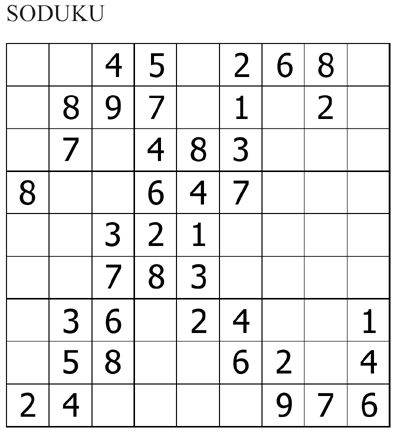
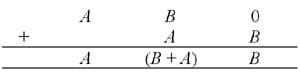1 Soduku
Click here for the answer.
2 Driven to distraction
A car leaves Coventry at the same time as a lorry leaves Leeds.
The car travels at 35 mph and the lorry averages 30 mph.
Which is further from Leeds when they pass?
Pull over and find the answer here.
3 A hairy problem
There are about 60 million people in the UK and none of those people have more than a million hairs on their head. Can you be sure that there are two people in the UK who have exactly the same number of hairs on their head?
To reveal the answer cut along here.
4 Count on algebra
Can you spot the mistake in this ancient algebraic balancing puzzle?
Two is equal to one – I don’t think so!
Where did it go wrong?
Click here for the answer.
5 Whether weather
At midnight it is raining hard in London. What is the statistical probability it will be blazing sunshine 72 hours later? We know the weather is unpredictable but perhaps you can work it out?
For the answer drop by here.
6 Superpower brain gain
Everyone can do a speedy multiply of a whole number by 10: you just move the digits one place to the left and put a zero in the units place. But you can prove your mental superpower by the speedy multiplication of any two-digit number by 11.
Stretch your imagination and learn how to train your brain’s double-digit dexterity here.

ANSWERS
1 Sudoku – Answer
ABOUT SUDOKU:
There are thousands of Sudoku puzzle books for sale and there are computer programmes that can generate seemingly endless puzzles for you. But will the Sudoku puzzles ever run out?
One way to look at this is to calculate how many ways there are to completely fill a Sudoku grid according to the rules. Mathematicians have tackled this problem and they worked out that there are 6 670 903 752 021 072 936 960 different possible Sudoku answers! That’s almost seven thousand billion billion!
Imagine that you can’t solve a hard Sudoku and so you start punching the ground. If each punch you make removes a single layer of atoms the area of your fist, then after 6 670 903 752 021 072 936 960 punches you will have made a tunnel right through the Earth that’s 8 metres wide! In short, we don’t have to worry about Sudoku puzzles running out anytime soon.
WHAT IS SUDOKU:
A Sudoku is a special type of Latin Square. A Latin Square is a square grid that is filled with a number of different symbols such that no symbol appears twice in any row or column. There have been implied uses of Latin Squares in both ancient Chinese and Islamic texts, but the first direct mention was from a 1723 solution to a card problem. (If you wish to try a similar card problem, try laying out all sixteen face cards from a deck in a 4 by 4 square so that every row and every column contains all four suits and all four faces: King, Queen, Jack and Ace.) So a Sudoku is a 9 by 9 Latin Square, with the extra condition that if this square is split into a 3 by 3 grid, each smaller box contains all 9 symbols.
USES OF SUDOKU:
While this may sound like a strange story of Sudoku puzzles in the post, it is exactly what your mobile phone does when you send a text. Your phone converts your text message into numbers (pretty much 1 for A, 2 for B etc), it arranges these numbers in a small grid and then expands it into a bigger grid using rules very similar to Sudoku. In fact all computers, satellites, digital radios and anything that sends information, does exactly the same thing. Then if any information gets lost, or an error in transmission causes some mistakes, this can be fixed by the receiving device as easily as solving a Sudoku!
Back to top
2 Driven to distraction – Answer
They are both the same distance from Leeds when they pass; they have to be as they are both at the same place!
Problem solving and lateral thinking are some of the useful skills that studying maths can teach you, training your brain to see what’s really important in a situation and what’s just distraction.
Back to top
3 A hairy problem – Answer
The simple answer is yes, there will be at least two people who have exactly the same number of hairs on their head. The reason is that there are more people (60 million) than the maximum number of hairs on a head (1 million). There are insufficient possible hair totals for everyone to be different; two must be the same somewhere.
Maths like this means we don’t need to go round counting the number of hairs on everyone’s head; we know the answer because we have a mathematical way to describe the problem. These sorts of mathematical ideas can help us understand more than just hairy heads. They are used in the field of medicine to help understand the spread of disease.
Back to top
4 Count on algebra – Answer
The mistake is right at the very end, when we did the division. We said at the start that a equals x, so (a – x) is zero and dividing by zero just doesn’t work mathematically. Think about it. How many nothings are there in something?
Many mathematical theories have come to an abrupt end because of this divide by zero problem. You can’t do it; if you try you get nonsense!
A well-known example of why this sort of algebraic error is important in the real world is the case of the US navy ship Yorktown. In its time it was state-of-the-art computer controlled but, in September 1997 while on manoeuvres, a crew member entered a zero by mistake into the ship’s software. The computer system couldn’t cope with this error and the computer control systems failed leaving the ship without any working engines for a few hours.
Understanding algebra helps make things safer.
Back to top
5 Whether weather – Answer
Weather is very hard to predict – that’s a fact! The mathematics used to work out where weather systems will be in the future are very complex but, as we know, it’s important. It can influence your choice of holidays and how many ice creams companies will buy. In this example, though, the answer is clear as day. 72 hours later it will be midnight again so there is zero chance it will be sunny. If only it was that simple for the mathematicians at the Met Office.
Back to top
6 Superpower brain gain – Answer
To give you this superpower, we make use of two things, one is maths and the other is the human brain’s power of imagination. To multiply any two-digit number by 11 at lightning speed, you need to use some visual imagery. Let’s take the number 52 for example. Now, imagine a space between the two digits, so in your mind’s eye you see 5_2. Add the two numbers together and imagine putting the sum of them in the gap in the middle: 5_(5 + 2)_2 and that is it, you have the answer: 52 × 11 = 5_(7)_2 = 572.
But what if the sum of the digits to go in the gap is itself a two-digit number? For example, if you want to multiply 98 by 11. You imagine 9_(9 + 8)_8 but that bit in the gap in the middle gives you 9 + 8 = 17, so where do you put these digits 9_(17)_8? Easy, just leave the second number (here the 7) in the gap as before and imagine moving the 1 up a place (9 + 1)_7_8 = 10_7_8 = 1079. Correct again!
Mathematicians make use of their imagination all the time. Our brains are really good at imagining things, at creating pictures in our heads, and often that’s the way we solve tricky problems or come up with clever visual imagination tricks like this one.
For those interested, the mathematics behind the scenes is fairly easy and is what allows us to have a visual picture in our imagination to do the calculation. Suppose you have the number AB (that’s A tens and B ones) and you want to multiply by 11. First you multiply by 10. That’s easy, AB × 10 = AB0. Then you add AB again (as 11 = 10 + 1). So you have the ‘digits’ A_(B + A)_(0 + B), which is exactly what all that sliding numbers around in your imagination has been doing without knowing it. Of course if the middle B + A is more than 10, that is, it’s a double digit, you just slide the first digit up to the hundreds column and it’s sorted.
For those who like formulae, this all boils down to:
Back to top
“