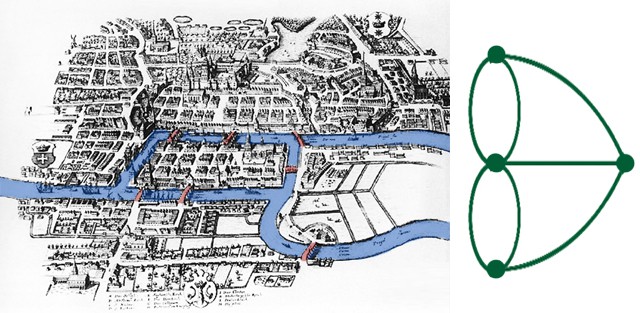
In the eighteenth century the city of Königsberg had seven bridges linking the different parts of the city. There was a debate among the citizens as to whether anyone could walk around the city crossing each bridge exactly once. Some people claimed that they had done it, but nobody could explain how.
It took one of history’s most famous mathematicians Leonhard Euler to prove that it was in fact impossible. By doing so Euler had written what is considered to be the first paper on Graph Theory, an area of mathematics which now has many important modern applications.
Firstly Euler reduced the map of the city to a diagram where each line represented a bridge and each dot represented a region of the town. Such a diagram is called a graph. Instead of walking around the city, Euler was now trying to show whether you could trace round the graph with a pencil, without having to go over any lines twice.
What Euler showed is that you must have an even number of edges coming out of each vertex (dot) for such a walk to be possible (except for the dots chosen for the start and finish). The reason is simple. When you go into a vertex by an edge, you must also leave again by another edge, so the number of edges must be even at each vertex. If such a path can be drawn on a graph then it is called an Eulerian Graph. If you were prepared to start and end at different vertices, then a graph could have two vertices with an odd number of edges, if you are starting and finishing your path at these vertices. Such a graph is called a Semi-Eulerian Graph.
In the case of Königsberg, every vertex has an odd number of edges coming out of it, so there is no way you can walk round the city crossing each bridge once and only once (thus it is neither an Eulerian or Semi-Eulerian Graph). The people who claimed to have done it must either have been mistaken or fibbing!
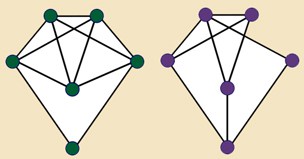
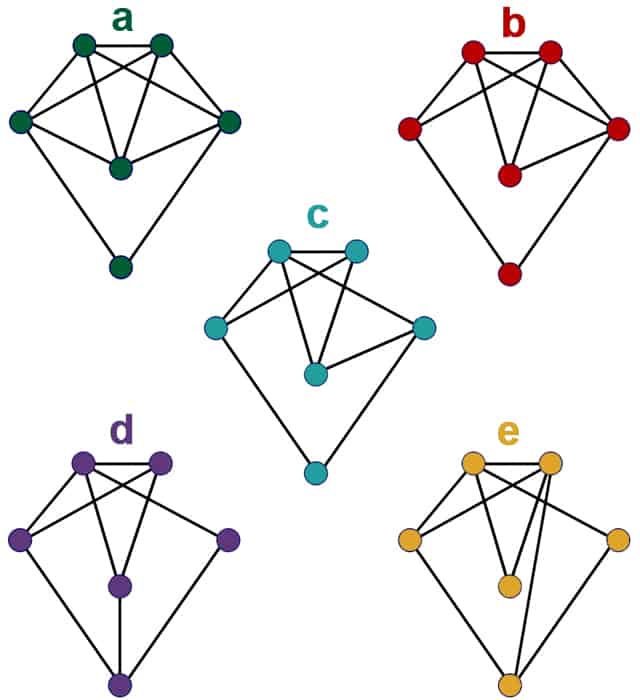
Have a look at the graphs below. Which ones do you think are Eulerian Graphs? (i.e. You can draw round them without taking your pen off the page and without going over a line twice, starting and stopping at the same vertex). Which ones do you think are Semi-Eulerian Graphs? (i.e. you can draw round them as you would with a Eulerian Graph, but not necessarily starting and stopping at the same vertex).
The first time you might start to study graph theory is while studying modules on Decision Mathematics at A-level. In fact Graph Theory and the study of Networks has become hugely important, particularly in computer science. When you think about it, lots of things can be pictured as graphs, ranging from transport systems, to electricity networks or even social networks such as Facebook or Twitter. Even the whole internet can be pictured as a giant network with billions of internet pages all linked together.
It may seem like Euler had solved a trivial problem relating to walking around a city. It is however often the case that mathematical discoveries which seem like they have no application often turn out to be really useful many years later.
Article by Hazel Lewis