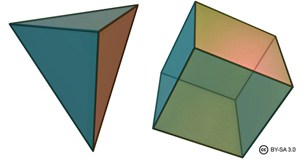
What is great about Euler’s formula is that it can be understood by almost anyone, as it is so simple to write down. Euler’s formula can be understood by someone in Year 7, but is also interesting enough to be studied in universities as part of the mathematical area called topology.
Euler’s formula deals with shapes called Polyhedra. A Polyhedron is a closed solid shape which has flat faces and straight edges. An example of a polyhedron would be a cube, whereas a cylinder is not a polyhedron as it has curved edges.
Euler’s formula states that for Polyhedra that follow certain rules:
F+V-E=2
Where F= Number of faces, V= Number of vertices (Corners), E=Number of edges
Let us check that this works for the Tetrahedron (triangle based pyramid) and the cube.
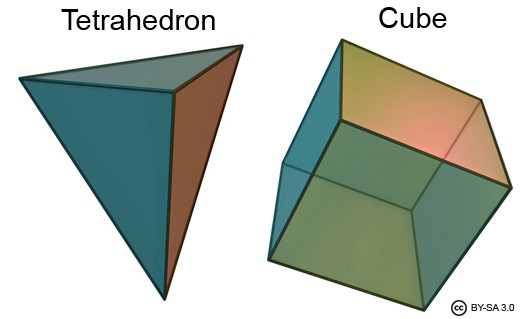
| Shape | Faces | Vertices | Edges | F+V-E |
| Tetrahedron | 4 | 4 | 6 | 4+4-6=2 |
| Cube | 6 | 8 | 12 | 6+8-12=2 |
Euler’s Formula does however only work for Polyhedra that follow certain rules. The rule is that the shape must not have any holes, and that it must not intersect itself. (Imagine taking two opposite faces on a shape and gluing them together at a particular point. This is not allowed.) It also cannot be made up of two pieces stuck together, such as two cubes stuck together by one vertex. If none of these rules are broken, then F+V-E=2 for all Polyhedra. Euler’s formula works for most of the common polyhedra which we have heard of.
There are in fact shapes which produce a different answer to the sum F+V-E. The answer to the sum F+V-E is called the Euler Characteristic χ, and is often written F+V-E=χ . Some shapes can even have an Euler Characteristic which is negative! This is where it can all start to get quite complicated. If you want to find about the Euler Characteristic of some of the strange shapes below, why not take a look here.
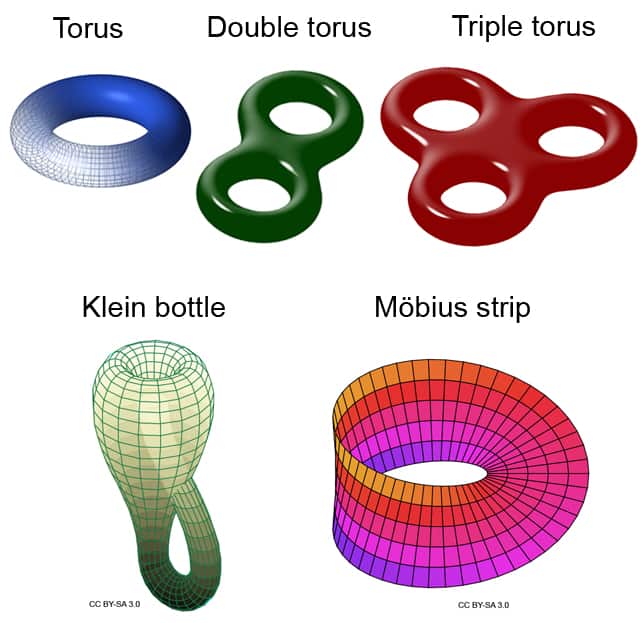
(If you have never heard of the Klein Bottle, click here to find out more. )
The Euler Characteristic helps us classify shapes and is studied as part of most undergraduate mathematics degrees as part of a topology course.
Can you now work out which of the following shapes should have an Euler Characteristic of 2?
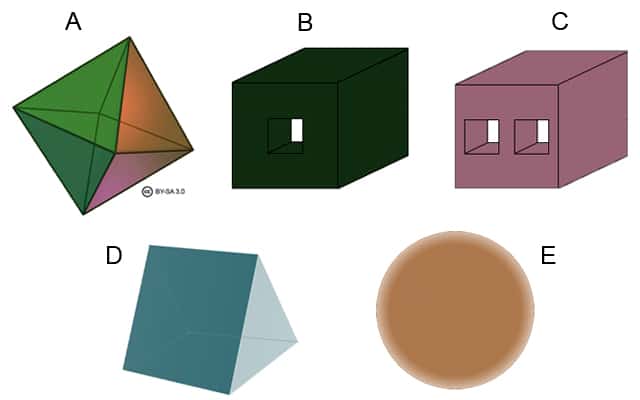
|
If you would like to find out more about Euler’s Polyhedral formula, including a proof, then take a look at this article in Plus magazine.
Article by Hazel Lewis