Can maths make things beautiful? There are certain geometric shapes and ratios that crop up again and again in art and nature. Artists and architects use these mathematical elements to make their work pleasing to the eye, while nature presumably has her own reasons for including it. One idea that has endured since ancient times is the Golden Ratio, also known as Divine Proportion.
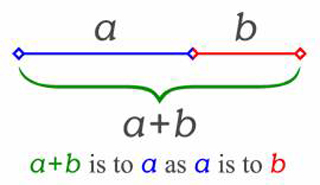
First described by Euclid, the ancient Greek father of geometry, the golden ratio can be drawn like this:
Any two lengths where a:b is the same as a+b:a are said to be in the golden ratio. These proportions have been encoded by artists and architects into their work for thousands of years. The ancient Parthenon in Greece shows these proportions, as do the works of Da Vinci, Dali, and more recently Mondrian.
The ratio can be expressed as a number, but it is not a rational number like 1, 42, or 7367; instead it’s like π, impossible to express exactly as a fraction. In fact, it has its own letter, φ. We can find φ using algebra:
![]() So aφ=b. Making the substitution and rearranging (you can work through the details yourself!) gives this rather pretty little number:
So aφ=b. Making the substitution and rearranging (you can work through the details yourself!) gives this rather pretty little number:
 That’s got some interesting properties of its own: in order to square φ, you just add one. This is a quadratic equation, since it involves a squared term. You will learn several different ways to solve a quadratic equation while you are in school. Trial and error is a good choice for now, or if you’re feeling ambitious you could try solving it algebraically. You’ll find that φ is 1.61803, or (√5+1)/2.
That’s got some interesting properties of its own: in order to square φ, you just add one. This is a quadratic equation, since it involves a squared term. You will learn several different ways to solve a quadratic equation while you are in school. Trial and error is a good choice for now, or if you’re feeling ambitious you could try solving it algebraically. You’ll find that φ is 1.61803, or (√5+1)/2.
There’s another totally different way to find φ: through a numerical sequence found in seed heads on flowers, bee populations and traditional Indian poetry. This is the pattern:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …
Can you see how it is made? Each term is the sum of the two previous terms. Nowadays we call this pattern the Fibonacci sequence, for the Italian scholar who documented it in Europe: and it is deeply related to φ. Taking the ratio between each term and the previous one gives this sequence:
1.000, 2.000,1.500, 1.667, 1.600, 1.625, 1.615, 1.619, 1.618, 1.618 (18recurring), …
The ratio converges to become φ! It turns out that the Fibonacci numbers are the nearest whole-number approximations to φ.
 So why are φ and the Fibonacci numbers found in so many places? Nature uses φ a lot because it spreads out growth enough to make sure resources get distributed well, but not so much that space is wasted. It’s possible that the reason people find the golden section appealing is because we recognise in it the beauty of the natural world. However, it’s worth remembering that if you try hard enough to find a pattern, you’ll probably do so! The diversity of places the golden ratio can be found is as much a tribute to the human imagination as the power of mathematics. But it remains a powerful inspiration to artists, musicians and mathematicians, who use its fascinating properties (many more than are listed here!) for work and play.
So why are φ and the Fibonacci numbers found in so many places? Nature uses φ a lot because it spreads out growth enough to make sure resources get distributed well, but not so much that space is wasted. It’s possible that the reason people find the golden section appealing is because we recognise in it the beauty of the natural world. However, it’s worth remembering that if you try hard enough to find a pattern, you’ll probably do so! The diversity of places the golden ratio can be found is as much a tribute to the human imagination as the power of mathematics. But it remains a powerful inspiration to artists, musicians and mathematicians, who use its fascinating properties (many more than are listed here!) for work and play.