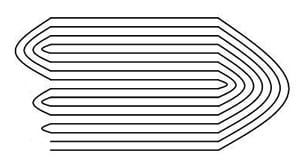
If you have ever repeatedly folded a sheet of paper, you will probably have been surprised at how few times it can be folded, with it quickly becoming a solid inflexible block which can’t be folded anymore. If the paper is thicker, it’s even more challenging! For many years it was thought that the maximum number of folds that could be achieved was just seven!
This was the case until when in 2002 American teenager Britney Gallivan demonstrated that a sheet of paper can be folded 12 times, provided that it is long enough and thin enough. Britney Gallivan demonstrated this by using a 1200m length of toilet paper, which provided her with both the length and thinness which she required. Ten years later in 2012 a group of students beat her record by taking 16km of toilet roll and folding it in one direction 13 times. Check out the video!
What is remarkable about Britney Gallivan is not only that she broke the record at the time, but also that she came up with an equation to show a theoretical minimum for how long the paper needed to be for a certain number of folds. For a strip of paper folded in a single direction, Gallivan came up with the following equation:
Where is the minimum required length of paper for
folds and stands for the thickness of the paper.
Finding the thickness of the paper ( )
)
To use this equation you first of all you need to know the thickness of the toilet paper which you are using. (Toilet paper has been selected as probably the thinnest paper which can actually be used without it breaking.) It is not easy to simply measure the thickness of your paper using a ruler. One intriguing way of calculating the thickness is as follows:
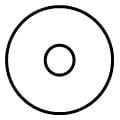
Imagine you have a toilet roll which you are looking at from the side. The area of this cross section will be equal to the length of your toilet paper multiplied by its thickness. ()
This cross section can also be worked out by using the following formula: where
is the diameter of the toilet roll and
is the diameter of the hole of the toilet roll.
We then have which rearranges to
.
If you then measure a typical toilet roll, you might find the following measurements:
Length
Diameter
Tube Diameter
When you put these numbers into the thickness equation we find that in the example above – you can try to find out how thick your own toilet roll is at home using this equation!
 Using Gallivan’s Equation
Using Gallivan’s Equation
Now that we have a thickness we can put some numbers into Gallivan’s equation. For 13 folds (the world record) and a thickness of 0.45mm we get a minimum required length of 15.8km to 1 decimal place. (Remarkably close to the 16km used in the actual record attempt.)
Now let us consider what we need to do in order to break this record and complete 14 folds.
Gallivan’s paper folding equation shows that we will need more than 60km of toilet paper in order to fold it in half the same way 14 times. It is hard to imagine how the students folded in half a piece of toilet paper 16km long, let alone 63.3km long. It may be some time before their record is broken!
| So what can we learn from all of this seemingly trivial mathematics of toilet paper? First of all that you are never too young to come up with some new mathematics of your own – Britney Gallivan was still at school when she invented her paper folding equation. Secondly that mathematics can be used to describe almost everything, from unimportant questions about toilet paper to how strong a bridge needs to be or how tall a skyscraper can be before becoming dangerous. Mathematics is literally everywhere you look. |
Article by Hazel Lewis