Have you ever tried to take the square root of a negative number on your calculator? On a normal scientific calculator you will be given an error message, implying that you have made a mistake in your calculation! In fact mathematicians often perform calculations with the square roots of negative numbers and call them imaginary numbers.
Why do we need imaginary numbers?
Whichever number you square, you will always end up with a positive answer, for example and
. Now if
, to find
you need take the square root of 16 (a positive number), and end up with two answers, one negative and one positive:
.
Mathematicians found that it is sometimes necessary to take the square roots of negative numbers, particularly when finding solutions to quadratic equations.
For example if we want to solve the quadratic equation we will probably try to use the quadratic formula. This leads us to two solutions
and we have the problem that we are trying to take the square root of a negative number. Mathematicians have therefore found it helpful to give the square root of a negative number a name, so that it can be worked with. The square root of minus
is called
. (Confusingly engineers call
as
already stands for current.)
So if we want to write as an imaginary number we would write
, or if we wanted to simplify our surd we would write this as
.
The word imaginary can be a bit misleading in the sense that it implies imaginary numbers don’t exist or that they aren’t important. A better way to think about it is that normal (real) numbers can directly refer to actual quantities, for example the number 3 can refer to 3 loaves of bread. Negative numbers can also be applied to debt, so that the number -200 could refer to being £200 in debt. Imaginary numbers simply don’t directly refer to any real quantities. However imaginary numbers do help for example in representing the magnitude and phase of electrical current – being called imaginary certainly doesn’t mean they aren’t important!
Complex Numbers
Most of the time mathematicians don’t work with imaginary numbers on their own, they use what are called complex numbers. Complex numbers are a combination of real numbers and imaginary numbers. For example would be a complex number as it has both an imaginary part and a real part. The complex numbers are of the form
where
and
are both real numbers. Confusingly
and/or
could be zero, meaning that real numbers are also complex numbers, as are purely imaginary numbers!
Complex numbers can be worked with in a very similar way to real numbers. Here are a few examples of the normal operations of addition, multiplication and division.
Addition
Simply group the real and imaginary parts together
Example:
.
Multiplication
Multiplying complex numbers is just like multiplying double brackets in algebra, remembering that .
Example:
Division
Division is a bit more complicated.
Example:
First represent your division as a fraction:
Then you need to multiply both the top and bottom of your fraction by the conjugate of the denominator which is in this case. This may remind you of rationalising the denominator when you are working with surds.
When we multiply out we are left with:
Which simplifies to:
Representing Complex Numbers
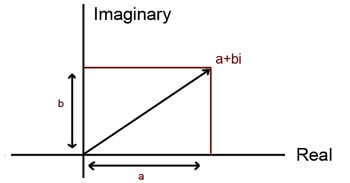
From early on in school, pupils learn to represent real numbers on a number line, so there is a question of where the complex numbers should live. Several mathematicians came up with the idea of representing complex numbers on a plane, with the real part on the axis and the imaginary part on the axis. The Complex plane is called an Argand diagram after a Swiss mathematician Jean-Robert Argand.
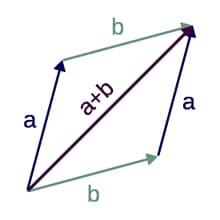
Now that complex numbers can be represented visually in this way, they can be thought of as vectors and can be calculated with using all our rules for manipulating vectors. To read a bit more about Argand diagrams click here.
As well as being enormously important in pure mathematics, complex numbers also have a large number of uses in the real world, including electrical engineering, and digital signal processing. The first time complex numbers are studied at school is usually as part of a Further Mathematics A-level, and after this anyone studying mathematics or engineering at university will be introduced to complex numbers. To read about more real world applications of complex numbers, take a look at the Wikipedia page on complex numbers.
The topic of complex numbers is a vast and interesting area of mathematical study. If you would like to read more articles on complex numbers, then you may wish to take a look at Plus Magazine’s library of articles on this subject.
Article by Hazel Lewis