Pi Day is celebrated around the world on the 14th of March each year. The reason for this is that the 14th March is written in the U.S. as 3.14 – the first three digits of π. While Pi Day might be a human invention, it is also a wonderful excuse to learn more about one of the most intriguing and spectacular numbers in the universe. To celebrate Pi Day this year we look at the story of Johann Lambert, a mathematician who provided one of the most important pieces of the puzzle in our understanding about π.
Lambert was a Swiss mathematician born in 1777 who rose from a humble background to become a great mathematician. As the son of a tailor, he left school at the age of 12 to take up work in the tailoring business. In his spare time in the evenings he continued his studies – learning about mathematics, physics and astronomy. This eventually meant that he could become a tutor in the house of a local Count and from there his extraordinary abilities were eventually noticed and he became a Professor of Astronomy.
While Lambert made many discoveries in astronomy and physics in his lifetime, he will always be best known for what he discovered about π.
What is π? A quick reminder
If you pick any circle and divide the length of its circumference by the length of its diameter you will always get an answer of π which is roughly equal to 3.14159 … This amazing fact is true for every circle in the universe, however it is only one of a number of incredible facts about π.
π – an irrational number
You have probably heard that if you write down π, it will go on forever without any repeating pattern:
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944…
This type of number is called an irrational number – it is a number which cannot be written down as a fraction and never ends when you start writing down its decimal expansion.
But how do we know that π is irrational and that it won’t end after a million, billion or even trillion digits? This was the extraordinary question which Lambert answered when he proved for certain that π is irrational. You will find at the end of this article an overview of Lambert’s proof.
π – a transcendental number
Lambert also speculated that π is what is known as a transcendental number. He didn’t manage to prove this fact – but it was eventually proved correct in 1882 by Carl von Lindemann. It was nonetheless a spectacular insight for Lambert to have spotted that π was transcendental.
So what is a transcendental number? Well, if we look at quadratic equations which have whole number or fractional coefficients such as:
Then we will be able to find solutions (real or imaginary) – in this case and
If a number is transcendental then it is not the solution to any quadratic equation in existence with whole number or rational coefficients, and it is also not the solution to any other similar polynomial either (containing , etc.) This makes π a pretty special number.
Therefore we should celebrate Johann Lambert this Pi day – the humble tailor’s son who went on to not only prove that π is irrational but also to tell the world that π is a transcendental number.
Remarkably if you look in the never ending digits of π you will be able to find any sequence of numbers, including your own birthday. Unfortunately Johann Lambert’s birthday appears at over 2 million digits into π, whereas someone born on the 1/5/92 would only have to wait a few digits to find their birthday hidden inside π. Why not look for your own birthday at www.mypiday.com
Background Information: Lambert’s Proof that π is irrational
How did Lambert manage to prove that π is irrational? Here is a brief technical overview.
First of all Lambert proved the fact that:
If is rational and not zero, then this means that
is irrational
Then Lambert used what is known as a contrapositive proof. This means that if you can say that A implies B, then you can also say that the opposite of B implies the opposite of A. For example if being 5 years old implies that you don’t have a job, then having a job implies that you aren’t five years old.
In our case we have:
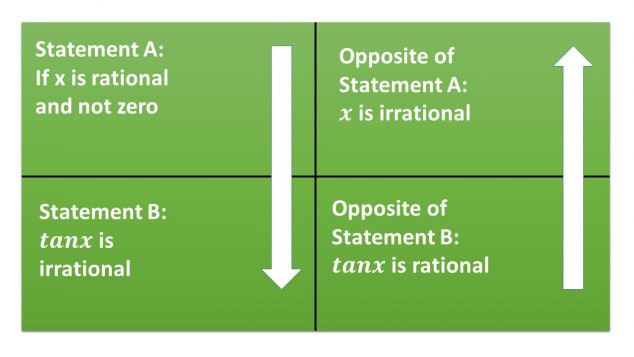
Lambert had proved that Statement A implies Statement B, therefore he had also shown the contrapositive, (Oppositive of Statement B implies Oppositive of Statement A):
If is rational then it implies that
is irrational
It was already known that is rational and equal to 1, therefore
must be irrational, and therefore
is irrational. Lambert had finally proved for certain that π is irrational.
Article by Hazel Lewis
Image Credit: Pi by Steve Rotman@Flickr






