In the aftermath of the worldwide banking crisis and widespread recession it is hard for a day to pass without some mention of the stock market.
As the ripples of recession spread around the globe share prices took a nose-dive. The collapse of the banks, however, was a very rare event. What about normal day-to-day trading? Patterns of behaviour in stock prices are not only big business but an important area of interest for mathematicians.
Those whose job it is to attempt to predict the stock market are market analysts. If they can predict what will happen to share prices in the future then they can either pull out their money if the stock is going to fall, or pump extra money in to capitalise from a rise. But how predictable is the stock market?
Market analysts generally fall into one of two camps: chartists and fundamental analysts. The basic assumption of a chartist is that history will always eventually repeat itself and so future prices depend on past prices in such a way as to give them a chance of judging what might happen.
Fundamental analysts work in a different way. They assume that an individual stock has an intrinsic value – what is actually worth in real terms. They use a series of factors to try and assess the value of this “equilibrium price” and see whether the current market value is above or below this price. Assuming everything moves towards equilibrium they can predict in which direction a stock price might move.
There will always be departures from the equilibrium price as there will a difference of opinion between traders as to what the stock is worth. However, the price is likely to oscillate above or below the true, unknown, equilibrium point.
But, both techniques work under the assumption that past performance has some bearing on future movement. The question mathematicians have been working to answer is whether these fluctuations are indeed systematic, and therefore partly predictable, or random and therefore not.
Here is a simple experiment to try. Imagine a new company is floated on the stock market at £10 a share. For each subsequent day toss a coin. If it lands on heads, increase the stock price by fifty pence. Should it land on tails, decrease the stock by fifty pence. Once you’ve done that draw a graph of stock price against time. Here’s an example we made.
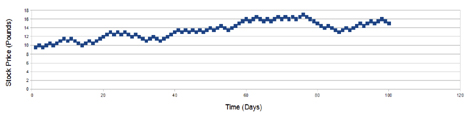
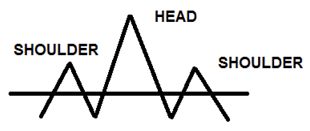
This graph looks very much like a typical stock chart. It even has some shapes that analysts spend a lot of time pouring over such as head and shoulder patterns. A head and shoulder pattern has two small peaks either side as shoulders with a greater peak in the middle for a head. Such a shape can be seen in our graph starting around the 16 day mark and finishing just before the 40th day of trading.
 In this random, coin-tossing scenario the direction of today’s movement had zero correlation to yesterdays’. In a more formal way mathematicians try to work out whether successive changes or price are correlated or whether, like the coin-tossing, they are independent. To do this they use an area of mathematics called “serial correlation coefficients” or “autocorrelation”. They perform a test to see whether current values of a stock price are correlated to past prices.
In this random, coin-tossing scenario the direction of today’s movement had zero correlation to yesterdays’. In a more formal way mathematicians try to work out whether successive changes or price are correlated or whether, like the coin-tossing, they are independent. To do this they use an area of mathematics called “serial correlation coefficients” or “autocorrelation”. They perform a test to see whether current values of a stock price are correlated to past prices.
Many studies have been published on the topic and the consensus of the research seems to suggest that the correlation is very weak – stock market fluctuations are random and very hard to predict. This means that a technique known as “buy-and-hold” where you just buy a stock and let randomness take its course should perform just as well as the chartists and fundamental analysts.
For more information on autocorrelation check out the pages on Wikipedia and Wolfram Alpha.
There is also a discussion of random walks in stock market prices here.






