Imagine you lived in a city which was laid out in a grid system, a bit like some American cities are. If you wanted to get to your friend’s house you might measure the distance, not as the crow flies, but as the distance you have to walk along the streets.
If you were to do this you would be using a special kind of geometry called ‘Taxicab Geometry’. The normal kind of geometry we use at school is called Euclidean Geometry. In Euclidean Geometry you measure the distance between two points as being the direct distance as the crow flies, whereas in Taxicab Geometry you are confined to moving along the lines of a grid.
Look at the diagram below. Using traditional Euclidean Geometry and Pythagoras’ theorem we measure the distance between A and B (the green line) as being 8.49 (2dp). If however we can only walk along the streets between our points, then the Taxicab distance between A and B is 12 units. Some possible paths of 12 units in length are illustrated below in red, blue and yellow. Taxicab geometry gets its name from the fact that taxis can only drive along streets, rather than moving as the crow flies.
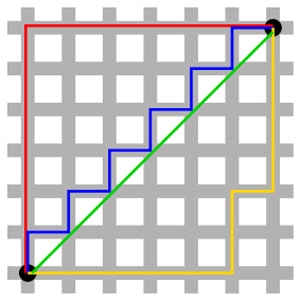
Euclidian Distance between A and B as the crow flies: 8.49units (Green).
Taxicab Distance between A and B: 12 units (Red,Blue and Yellow).
Formal definition of the Taxicab Distance.
Suppose you have two points 
and 
then:
Taxicab Distance between  and  |
The function which is shown with two straight lines is called the modulus and means that we take the positive value of whatever is inside it. So for example the value of 
is just 3 and the value of 
is also just 3.
Example
The Taxicab distance between 
and 
would be 
The Taxicab World
Now we can imagine that we live in a world where everything is measured using Taxicab distances. What would familiar shapes look like? It is quite surprising when we start to investigate.
The Circle in the Taxicab world
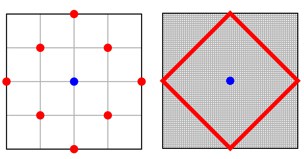
We can define a circle to be the set of points which are a constant distance from a centre. For example if we take all the points which are a distance of 4 units from a point A, then we have a circle of radius 4 with a centre at point A. In the Taxicab world this turns out not to look like a circle but a square! If you look at the red points on the diagram on the right then they are all 4 Taxicab units from the blue centre point using the Taxicab distance.
Value of π in the Taxicab world
If we take π to be circumference 
diameter then in the Taxicab circle above we would calculate the circumference to be 32 and the diameter to be 8, giving a value for π as 4. This turns out to hold for all Taxicab circles!
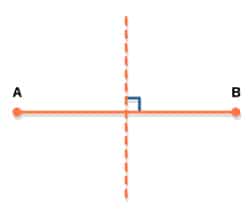The perpendicular line bisector
When using the Euclidean measure of distance the perpendicular line bisector is simple to draw. It is defined as being the set of points which are an equal distance from two points. In the diagram on the left, all the points on the dotted line are an equal distance from points A and B:
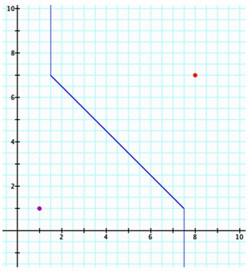Using the Taxicab measure, the perpendicular line bisector is a really surprising shape. The points on the line on the right are an equal distance from the two points using the Taxicab measure of distance.
However the configuration above is just one possibility. Have a play around with the points A and B in the geogebratube interactivity below and you should find a surprising result. There are some places for A and B which produce a perpendicular line bisector which is not just a line, it also includes a whole region of points! Can you find them?
Created with GeoGebra – Shared by Steve Phelps – Share or copy
One of the wonderful things about Taxicab geometry is that you can keep on investigating all manner of shapes and geometrical properties. You might want to investigate what an ellipse might look like or even a parabola within the Taxicab world.
If you would like to have a go at completing a worksheet on Taxicab Geometry, one can be found here.
There are even some useful applications to Taxicab Geometry with some researchers using it when modelling the spread of fire within a grid based system.
Article by Hazel Lewis
