The kissing number
In mathematics the ‘kissing number’ is defined as the largest number of circles which can touch another given circle of the same size. You can find the solution easily by using coins. It is pretty obvious that only six coins can touch another central coin at one time.
Therefore in two dimensions (mathematically known as being ‘in the plane’), the kissing number is six. In mathematics it isn’t enough to just show that one particular solution works, we need to prove that six is the maximum number, and that there can’t be a clever way of using seven or more coins.
Proof that the kissing number is six in the plane.
Let us label the centre of our central red circle as and the centres of our surrounding circles as
…
Let us now imagine that we have got more than six circles surrounding our central circle. Now let us draw in the triangles with vertices . (See the diagram below.) In the triangle
the edges
and
both have length
where
is the radius of the circle.
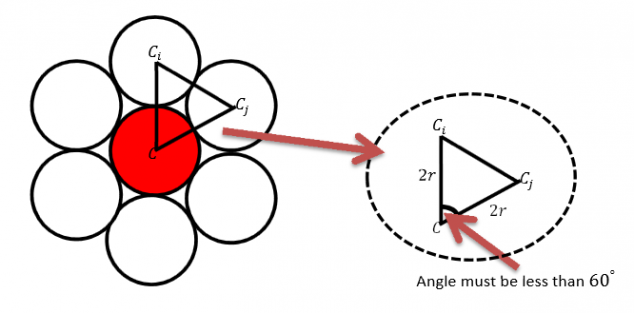
There are in a circle which means that if there are seven or more outside circles, then there has to be at least one of these triangles which has an angle
which is less than
.
This makes the triangle an isosceles triangle. It also means that the length
must be less than
This is because the longest edge in a triangle is always opposite the largest angle.
If is less than
then the other two angles will be greater than
and
will be bigger than the length
.
If is less than
in length then this means that the circles must overlap which is not allowed!
We have used a method known as proof by contradiction to show that it is impossible to have more than six circles surrounding a central circle.
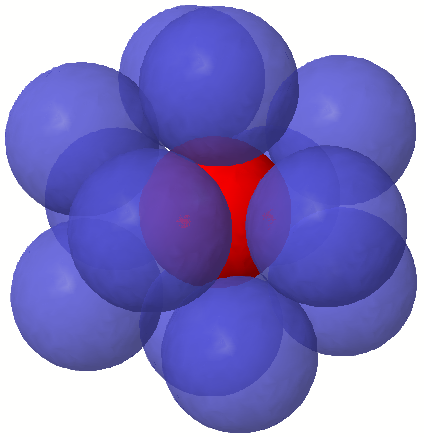
The kissing number in 3D.
In three-dimensions, the kissing problem requires us to find the maximum number of spheres which can touch a central identical sphere. There was a famous disagreement between Isaac Newton who thought that the answer was 12 spheres, and another mathematician, David Gregory, who thought that the answer was 13 spheres.
It took hundreds of years for mathematicians to come up with a proof. In 1953 Isaac Newton was finally proved right when the kissing number in three-dimensions was proved to be 12. There is still a lot of space left over, so you can see why people thought that you can fit more than 12 spheres around a central sphere.
Kissing numbers in other dimensions.
Mathematicians have also worked on kissing numbers in other dimensions, and there are still many kissing numbers which haven’t been found yet.
Here is a summary of the first ten dimensions.
| Dimension | Kissing Number |
| 1 | 2 |
| 2 | 6 |
| 3 | 12 |
| 4 | 24 |
| 5 | Not known – between 40 and 44 |
| 6 | Not known – between 72 and 78 |
| 7 | Not known – between 126 and 134 |
| 8 | 240 |
| 9 | Not known – between 306 and 364 |
| 10 | Not known – between 500 and 554 |
To find out more read this Plus Magazine article on Newton and the kissing problem.