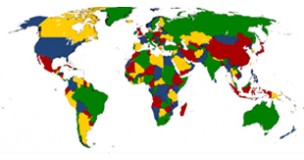
As anyone who’s scribbled down row after row of calculations knows, mathematical problems can take a long time to solve. If you thought homework was bad enough, imagine being Kenneth Appel or Wolfgang Haken. Their problem was so long that only a computer could solve it, and their proof can never be checked manually by any human mathematician. What was all the fuss about? How to colour in a map – otherwise known as the Four Colour Theorem.
Is four enough?
It all began in 1852, when a mathematician and botanist named Francis Guthrie was colouring in a map of the counties in Britain. He was trying to avoid using the same colour on any adjacent counties, and realised he needed at least four colours to do so. Guthrie wondered whether it was possible to draw a map that required more than four colours to avoid identically coloured neighbouring regions. He asked his brother Frederick, also a mathematician, who spread the question to the wider mathematical community. No one had an answer.
The puzzle remained unsolved until 1879, when an English mathematician named Alfred Kempe published a proof in the American Journal of Mathematics. Unfortunately the proof only lasted until 1890, when Percy Heawood spotted a flaw in the logic. Using Kempe’s work, Heawood was able to show that no more than five colours were needed, but the Four Colour Theorem remained unproven.
Drawing a blank
So why was this a job for computers, not crayons? It’s easy to show that three colours or less aren’t enough to fill in a map – take a look at this simple example:
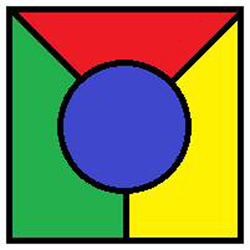
Attempting to draw a five colour map quickly leads to problems though. No matter how you try, all maps seem to be fully coloured by just four shades. But how do we know there isn’t some incredibly complicated map out there, a counterexample lurking in the the colouring box? Proving the Four Colour Theorem means showing that such a counterexample can’t exist, and to do that we need a way of describing maps mathematically.
We normally use the world “graph” to describe diagrams like a bar or pie chart, but a mathematical graph is a set of points joined together by lines. These points and lines are called vertices and edges, and it turns out we can convert any map in to a graph by drawing the regions as vertices and the boundaries as edges. For example, here is the map shown above drawn as a graph:
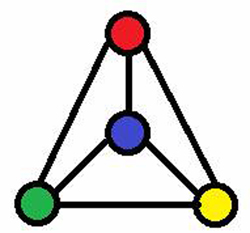
Turning maps into graphs means we don’t have to worry about their actual shape, and can concentrate on the relationship between regions. Mathematicians in the early 20th century used the techniques of graph theory to show that any map with less than a certain number of regions would only ever need four colours – but that still left an infinite number of maps to check!
Finding a shortcut
What mathematicians needed was a way of reducing this infinite number to something more manageable. In 1976 at the University of Illinois, Kenneth Appel and Wolfgang Haken were able to prove that any map could be reduced to a set of 1,482 basic types. They realised these building blocks could be used to make any map imaginable, so if all 1,482 only needed four colours, then so did every map.
There was just one problem. Checking these 1,482 maps would be an impossibly long task for even an army of mathematicians to complete. Instead, Appel and Haken programmed a computer to do the colouring. The analysis took 1,200 hours of computer time, but after a long wait came the result: all 1,482 maps required just four colours. Francis Guthrie’s simple question had been answered, a century after he first proposed it.
It wasn’t a question that particularly needed an answer – after all, mapmakers had happily been colouring in for years – but the Four Colour Theorem is important for a couple of reasons. The work on graphs helped define an area of maths called topology, which is used to study everything from the shape of the universe to the movement of robots. More significantly, the Four Colour Theorem marked the first major use of a computer in a mathematical proof. Many mathematicians were unhappy that only another computer could examine the full proof for errors. What if there was a bug in the software, or a faulty piece of hardware? Exhaustively running through every possible combination also didn’t seem “proper” to some mathematicians, as it gave the correct answer but not a true understanding of the problem. Computers have since been used to prove many other theorems, but their use raises questions of what it really means to “do” mathematics.