Mathematics is the purest of the sciences, dealing in eternal truths and abstract ideas. As such, most mathematicians prefer to avoid messy, organic details, such as corals, lettuce and household crafts. But welcoming these foreign objects has produced great results in the oldest branch of maths – geometry.
Accepted geometry
For 22 centuries Euclid (fl. 300 BC, Alexandria) was the authority on geometry. His most famous writing condensed all the geometrical knowledge of the time down into five axioms, from which the whole of geometry could be reconstructed. Four of these axioms are simple, describing such ideas as the existence of a straight line between two points and the circle. The fifth one, the ‘parallel postulate’, was the tricky one.
There are many ways of expressing the parallel postulate. Perhaps the simplest is that through a point not on a given straight line, at most one line can be drawn that never meets the given line. To mathematicians, this idea seemed less elegant than the others, and for centuries they tried to prove that it followed, somehow, from the first four. None were successful.
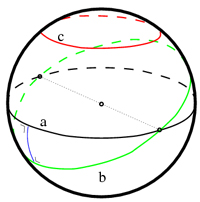 Around 1830, the Hungarian mathematician János Bolyai and the Russian mathematician Nikolai Ivanovich Lobachevsky separately cracked this nut, demonstrating that the fifth postulate is not as general as the others. It is only true if the surface on which it is being done is flat. If the surface is spherical, then there are no straight lines that can be drawn through the point without eventually converging.
Around 1830, the Hungarian mathematician János Bolyai and the Russian mathematician Nikolai Ivanovich Lobachevsky separately cracked this nut, demonstrating that the fifth postulate is not as general as the others. It is only true if the surface on which it is being done is flat. If the surface is spherical, then there are no straight lines that can be drawn through the point without eventually converging.
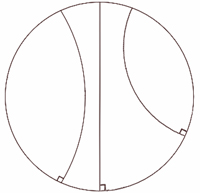 If the surface is hyperbolic, then an infinite number of lines can be drawn, which will never meet the original line. Spheres and flat planes are an easy way of visualising and interacting with these forms of geometry. But the hyperbolic plane is unfamiliar and inaccessible.
If the surface is hyperbolic, then an infinite number of lines can be drawn, which will never meet the original line. Spheres and flat planes are an easy way of visualising and interacting with these forms of geometry. But the hyperbolic plane is unfamiliar and inaccessible.
Hyperbolic space has many hard-to-visualise properties. It grows exponentially. It has negative curvature throughout. The angles in a triangle on a hyperbolic surface add up to less than 180. We know of shapes where a portion of their surface is hyperbolic – saddles and horns are often mentioned – but nothing that is hyperbolic throughout. Many thought it was impossible to model, and should just be represented in the abstract.
Crochet yourself a universe
That was until a Latvian professor of mathematics at Cornell University in the US – Daina Taimina – brought her knowledge of crafts to the subject. Using crochet, she created a variety of hyperbolic planes (see images). To non-mathematician’s eyes these models look organic – like coral reefs, lettuce leaves and sea slugs. For years mathematicians had been racking their brains to envisage this shape, while these creatures and plants had been merrily growing in it. Why didn’t anyone notice this? When asked, one guy said he ‘didn’t spend much time looking at sea slugs’.
 Perhaps they should have. Visualising the hyperbolic plane helps us get our heads round non-Euclid geometry – which is necessary to get a handle on the future and shape of nothing less than the shape of the universe.
Perhaps they should have. Visualising the hyperbolic plane helps us get our heads round non-Euclid geometry – which is necessary to get a handle on the future and shape of nothing less than the shape of the universe.
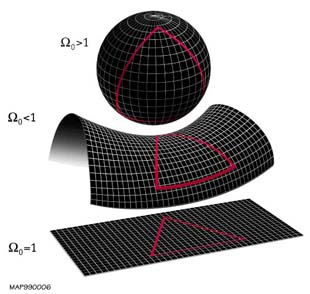
Our universe began at one point, and has been expanding ever since. Whether this expansion will continue for ever, or one day halt and come crashing back in, depends on the amount of matter that exists. If there is enough matter, the force of gravity will eventually overcome the expansion and drag everything back together in a big crunch. If there is not, the universe will continue outward forever. And an in-between option is also possible: that there is just enough matter to slow the expansion down to a continuous rate, but not enough to collapse the universe.
According to general relativity, the presence of matter distorts space time into a different geometry, so each of these matter densities gives a different shaped universe. A universe with a large amount of matter will be curled around on itself into a hypersphere, the 4D equivalent of a 3-sphere, and will obey spherical geometry. This is a ‘closed’ universe. It is finite in extent, but unbounded – if you go in one direction long enough, you’ll end up where you began. On the other hand, if there is definitely not enough matter in the universe to close it up, it is known as an ‘open’ universe. There are many more shapes this universe could take, but they’re all hyperbolic. If there’s just enough matter to balance the expansion, this in-between case corresponds to Euclidean plane geometry.
NASA’s current measurements suggest the universe is flat to a two per cent margin of error – so despite the twisted ideas of Bolyai, Lobchevsky, Taimina and the sea-slugs, Euclidean geometry may be the ultimate bottom line.






