Darts

Darts is a tricky game – it punishes the greedy amateur. If you’ve ever watched a professional darts match then you’ll have seen the world’s top players consistently and successfully aiming their arrows at the twenty area at the top of the board. Try and replicate this for yourself though and you might well end up in the adjacent slices, scoring you a measly five or one respectively.

The game of darts is all about accuracy and reliability of throw. So what if you find yourself not being able to hit those twenties time and time again? Can mathematics be used to give you an edge over your opponents?

One thing to look at is what you can score with very little effort, in fact the absolute minimum effort: not even aiming.

Let’s assume that you throw a single dart towards the board at random. To make things easier let’s ignore the black area just outside the scoring area and assume your un-aimed dart hits the scoring part somewhere. What sort of score are likely to achieve employing this seemingly lacklustre technique?

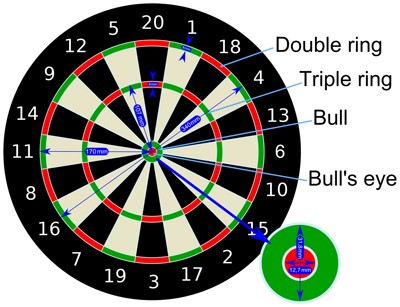Image licensed under a CC 3.0 licence by Fornax.

First we need to look at a standard dart board (and its dimensions) which are summarised in the diagram above. The small outer ring (which is 8mm thick) doubles your score for that slice i.e. hitting the red slice just below the number 20 scores you 40. The similarly wide small division in the middle of each number trebles your score. Hitting the green area right in the centre of the board (called the “outer bullseye” or “outer bull”) scores 25. The red “bullseye” right in the centre scores you 50.

The area of each of these sections is summarised in the table below. The area of a circle is π × radius² and the ? has been retained in each case as they will neatly cancel later on.

Section	Radius (mm)	Area (mm2)
Whole scoring area	170	28900?
Double ring	N/A	28900?
Treble ring	N/A	28900?
Outer bull	15.9	252.8?
Inner bull	6.35	40.3?
Singles area	N/A	24302.9?

The areas for the double and treble rings were calculated by finding the difference in area between the circles described by their inner and outer edges. The double ring is 8mm thick and so its area is π(170² – 162²) mm². Similarly the area of the treble ring is π(107² – 99²) mm². The area of the singles area is simply the area of the whole scoring area minus all the other areas.

If you throw a dart at random, which is guaranteed to hit some part of the scoring area of the board, what are your chances of hitting each section? The answer is simply the percentage of the board that that section represents. These values are summarised in the table below (NB this is why π was kept in: they cancel out when you divide the two areas).

Area	Fraction of whole board / % chance of hitting
Singles	~ 84%
Doubles	~ 9%
Trebles	~ 6%
Outer bull	~ 0.9%
Inner bull	~ 0.14%

Now we need to look at the average single dart score likely over many throws for each of these areas. This is done by adding the lowest possible score to the highest possible score and dividing by two.

Area	Lowest single dart score	Highest single dart score	Average
Singles	1	20	10.5
Doubles	2 (Double 1)	40 (Double 20)	21
Triple	3 (Treble 1)	60 (Treble 20)	31.5
Outer bull	25	25	25
Inner bull	50	50	50

Note that the scores for the last two areas are fixed.

To work out what the average single dart score will be when throwing at random all that is left to do is multiply the average score for each section by the chances of hitting that section. Then add all the sections together.

This is:

(10.5×0.84) + (21×0.09) + (31.5×0.06) + (25×0.009) + (50×0.0014) = 12.9

As each turn consists of throwing three darts, the average score per turn is 12.9 × 3 or 38.7.

The simple truth here is that if, more often than not, you are scoring less than 39 with your three darts then you are more likely to play better by throwing your darts at random! If you’re tempted to always aim for twenty and end up languishing in the ones and fives, close your eyes and try again.

However, aiming for the twenties is the best technique if you have an accurate enough throw. But how do you know how accurate your throw is? Mathematicians at Stanford University in the US have come up with a way for you to find out.

They looked at where your dart was likely to end up compared to where you actually aimed it. For this they used a Gaussian distribution. For professional players the variance would be very small, for amateur players it will be higher. Knowing your variance, would give you a head start in knowing where to aim to maximise your score.

Ryan Tibshirani, Andrew Price and Jonathan Taylor did just that using an Expectation–maximization algorithm. Their algorithm allows you to enter the actual scores you achieve when aiming for the bullseye. If you enter 50 scores (i.e. you need to throw at the bullseye 50 times) their algorithm provides you with an estimation of your variance.

The moral of the story is that if you’re not particularly good at darts but you want to improve without hours of practice, don’t copy the pros, listen to the mathematicians.

For a more in-depth looks at the work of Tibshirani, Price and Taylor visit their A Statistician Plays Darts page.