Paul and Guy both work at the same company, and car share to get to work. They also enjoy nights out during the week. Because of this they sometimes have a hard start the next morning. One Friday morning, they arrive two hours late, and claim that they had a flat tyre.
Their boss, Gabriel, isn’t convinced by their excuse, and asks them to separately write down which tyre was the flat one. They have to do this without communicating with each other.
If they made up the story about the tyres, how likely is it that they will both give the same answer?
Answer to part 1
Guy has a ¼ chance of picking one of the tyres.
For a particular tyre that Guy picks, Paul has ¼ chance of picking the same one.
Therefore, for each tyre, there is a 1/16 chance that they will both pick the same tyre.
Hence over all 4 tyres, there is a 4/16 chance that they will both pick the same tyre.
The answer is therefore ¼
Answer to part 2
The probabilities for all possible scenarios are as follows:
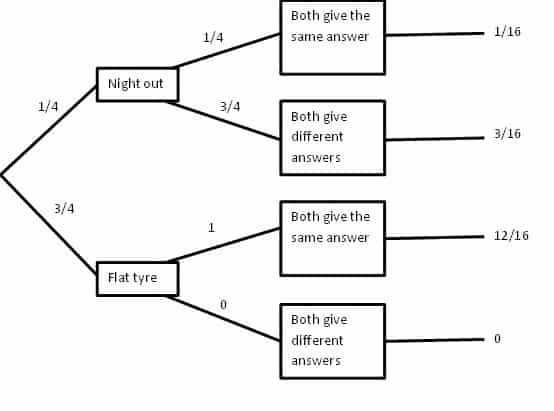
There is a 1/16 chance that Guy and Paul will be able to fool Gabriel into thinking they had a flat tyre, when in fact they didn’t. In all other cases, Gabriel will be able to figure whether they really had a flat tyre or not. Therefore one possible answer to this question is that, the likelihood that this test will allow Gabriel to identify whether they really had a flat tyre or not is 15/16.
However, if we take the question literally and only want to know the likelihood that the test will allow Gabriel to identify whether they really had a flat tire (i.e. without the “or not” phrase), then the answer is different.
This is because if Guy and Paul selected different tyres during the test, then Gabriel will know that they definitely didn’t have a flat tyre.
Therefore, if the tests suggest that they really had a flat tire (i.e. if they both give the same answer), then 12 out of 13 times they will have actually had a flat tire and are telling the truth. Therefore, if they both give the same answer, then there is a 1 in a 13 chance that they are lying.
Hence, the likelihood that this test will allow Gabriel to identify whether they really had a flat tyre is 12/13.
This question, therefore, has at least two possible answers, as it was not made clear if the negative result (i.e.. the test confirming that they didn’t have a flat tire) should be considered or not.
This kind of result is quite normal for practical problem solvers who use maths to help businesses. They do not always have the problem statement clearly defined. To start to develop a solution to a real-world business problem they have to make certain assumptions. These assumptions are then updated as the results are analysed.







