Over 90 teams. More than 2000 matches. A game of two halves. Fans often grumble when their squad is scheduled for a midweek kick-off hundreds of miles away, but the numbers involved make producing football fixtures difficult. Factor in trying to keep everyone happy – the clubs, the police, the media, local councils, and of course the fans – and the problem becomes even harder. Thankfully, maths can help. By following mathematical rules known as algorithms, league organisers can come up with the best possible fixtures lists.
Five-a-side fixtures
Suppose we want to generate fixtures for a small league, with just six teams. Each team must play every other team twice – home and away, which means 30 matches. (Why 30? Use the permutations formula to find out)
We could just write down these matches in any order, but that might easily lead to a mistake like scheduling the same team twice on one day. It’s much better to approach the problem logically, using an algorithm known as the ‘polygon method’.
For a league with N teams, we begin by drawing an (N-1) sided regular polygon. For our example six-team league, that means a regular pentagon. Each vertex, along with the centre point, corresponds to one team.
Next, draw lines between the horizontally aligned vertices and the top/centre points. These lines show the fixtures for the first matches.
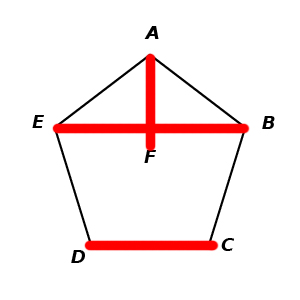That means that E plays B, D plays C, and A plays F. To find the matches for subsequent rounds just rotate the pentagon and repeat the process.
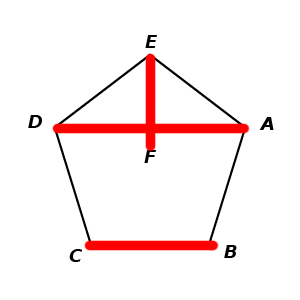In the second round, D plays A, C plays B and E plays F. After five rotations of the pentagon, we return to the start and end up with the following table:
Round |
Match 1 |
Match 2 |
Match 3 |
1 |
E vs B |
D vs C |
A vs F |
2 |
D vs A |
C vs B |
E vs F |
3 |
C vs E |
B vs A |
D vs F |
4 |
B vs D |
A vs E |
C vs F |
5 |
A vs C |
E vs D |
B vs F |
These fifteen matches are only half the fixtures, but this is easily solved by having the teams run through the same sequence, swapping the home and away team. Our simple league is ready to kick-off.
The big leagues
Real-life fixtures are also designed using logical algorithms, but the maths involved is more complicated. While the polygon method is useful for smaller leagues like in our example, it can’t handle the requirements of the larger Premier and Football leagues.
There are various restrictions on who can play when. Certain teams are paired up and are not allowed to both play at home on the same day, to avoid having too many football fans in one location. For example, Manchester United and Manchester City are paired so that Manchester doesn’t grind to a halt on match days! Clubs may also wish to avoid hosting big matches on certain dates – like Cheltenham, who often request that their games don’t clash with the town’s famous horse racing festival.
With all of these rules and requests in mind, designing the football fixtures table becomes a process of optimisation. Unlike many other mathematical questions, there is no ‘correct’ answer to an optimisation problem. Instead, you try to find the best solution that satisfies as many constraints as possible. One way is to use a ‘branch-and-cut’ algorithm, which creates a ‘tree’ of possible solutions, and then cuts off branches that don’t fit the requirements. A computer does the number crunching, but the results are often hand-tweaked to find the most suitable solutions.
Give it your best shot
Designing football fixtures is just one of the many applications for optimisation techniques. Manufacturing, business management, or anything that involves scheduling and planning all require the ability to examine a problem, work out the constraints, and come up with the best possible result. Whichever area you work in, it pays to have maths on your team.
