How well do you know the Square Root of 2? It might not be as famous as Pi, or Euler’s Constant (e), but it still has many interesting properties and a whole history of its own.
Who Discovered the Square Root of 2?
One of the best pieces of evidence for the ancient use of the Square Root of 2 is in a Babylonian Clay Tablet which is over 3500 years old. In the picture of it below, it has been labelled so that we can see the number 1 24 51 10 across the diagonal of the square. This is a number written in Base 60 and represents
Type the Square Root of 2 into your calculator and you will get 1.414213562 – the Babylonians were working to an accuracy of six decimal places. This advanced knowledge of the Square Root of 2 certainly suggests that it wasn’t a new discovery and had been in use for many years before that.

The Square Root of 2 – It’s Irrational
An irrational number is one which cannot be written as a simple fraction (a ratio of two whole numbers). If you write out an irrational number, it has a decimal expansion which will go on forever and ever without repetition. It is thought that the irrationality of the Square Root of 2 was discovered by the Pythagoreans who lived around 2500 years ago.
Hippasus of Metapontum and the Fear of the Irrational
It is thought that the irrationality of the Square Root of 2 upset Pythagoras and his followers who thought all objects could be represented by whole numbers and their ratios. There are many legends which surround the fate of Hippasus of Metapontum, who was credited with the discovery of this irrationality. Was he drowned at sea or was he simply expelled from the Pythagorean sect? Did he even discover the irrationality of the Square Root of 2 at all?

It is highly likely that much of this is legend, but perhaps these stories play into a deep disquiet which many people still have regarding irrational numbers.
Where Did the Word ‘Surd’ Come From?
The Square Root of 2 is a type of surd. Other examples of surds include or
, but would not include
as this has a rational answer
.
According to the Merriam-Webster dictionary, the word surd in this mathematical context was first used in 1557 and comes from the Latin word ‘surdus’ meaning deaf, silent or stupid. It seems that surds were still seen as not to be trusted – even 2000 years after Pythagoras.
Proof That the Square Root of 2 Is Irrational
There are many different proofs that the Square Root of 2 is irrational. Here is one of the most famous ones:
Step 1. Assume that is not irrational, and that it can be written as a fraction in its simplest form:
where a and b are whole numbers (non zero), and where
cannot be cancelled down any further (meaning it is an irreducible fraction).
Step 2. Square both sides of the equation and rearrange:
Step 3. This now means that must be an even number and also that
itself must also be an even number. Therefore you can rewrite
with
being an integer. Substituting this into the line above gives:
By the same reasoning as before this means that is an even number and we can write
, with
an integer.
Step 4. We had that , but we have shown that both
and
are even which means that
can be cancelled down, meaning that it is not an irreducible fraction. This contradicts our assumption in Step 1 that
is in its simplest form. This is what is called a proof by contradiction.
is irrational!
How Is the Square Root of 2 Different From Pi?
Both Pi and the Square Root of 2 are irrational, but there is an important difference – Pi is classed as a Transcendental Number, whereas the Square Root of 2 is not a Transcendental Number. If you like Venn Diagrams, then the following image might be helpful in showing that only some of the irrational numbers are also transcendental.
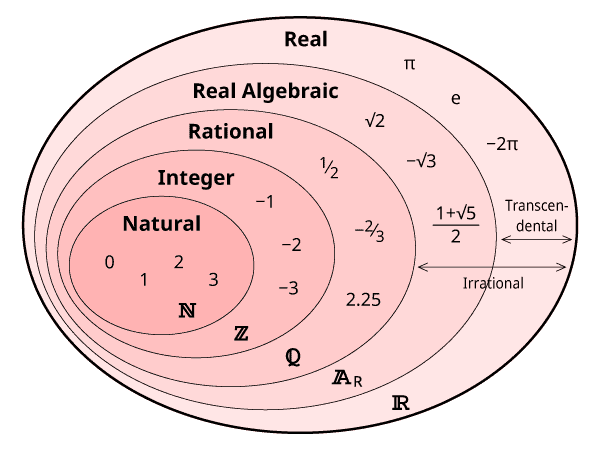
So what is an Algebraic Number? To be Algebraic, a number must be a root of a non-zero polynomial equation with rational coefficients. For example, if you solve , then
is a root. You can’t do this with Pi, it is Transcendental.
The Gelfond-Schneider Constant
Unlike the Square Root of 2, The Gelfond-Schneider Constant is a transcendental number (it is not a root of any non-zero polynomial equation with rational coefficients). If you raise the Gelfond-Schneider Constant to the power of
then you get back to a whole number answer of 4!
How Do Computers Calculate the Square Root of 2?
Most computers use the Newton-Raphson method which is commonly taught at A-Level, applying it to solve . Here is the iterative formula which is used:
If we let then we have:
Within 5 steps this gives us an estimate for which is as accurate as the full display on a standard calculator.
The Connection Between a4 Paper and the Square Root of 2
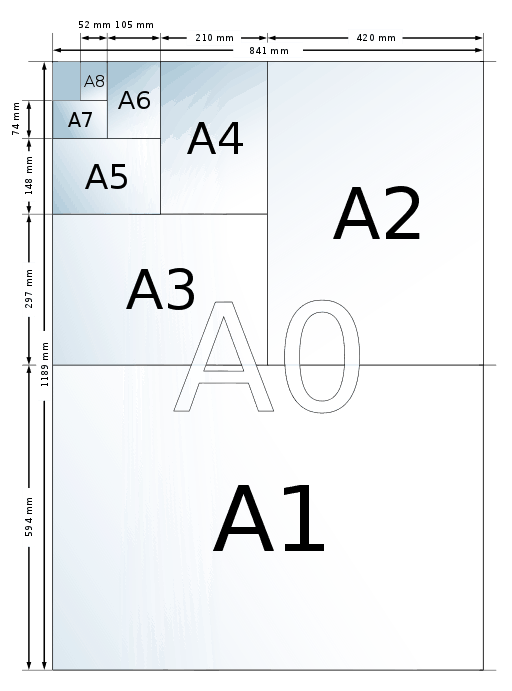 The largest sheet of paper in the A series is A0, with dimensions of 1189mm to 841mm. A0 is almost exactly 1 square metre in area. If you cut an A0 piece of paper in half you will get two pieces of A1 paper, each with an area of half of a square metre. After this, the pattern continues – cut an A1 piece of paper in half and you will get two pieces of A2 paper, each with an area of a quarter of a square metre. This makes document stacking and reproduction cheaper and more efficient, but what is good about this system is that it also keeps the length/width ratio of the paper sizes consistent. If you blow up a poster from A4 to A3, you want it to fit exactly – you don’t want to be cutting bits off!
The largest sheet of paper in the A series is A0, with dimensions of 1189mm to 841mm. A0 is almost exactly 1 square metre in area. If you cut an A0 piece of paper in half you will get two pieces of A1 paper, each with an area of half of a square metre. After this, the pattern continues – cut an A1 piece of paper in half and you will get two pieces of A2 paper, each with an area of a quarter of a square metre. This makes document stacking and reproduction cheaper and more efficient, but what is good about this system is that it also keeps the length/width ratio of the paper sizes consistent. If you blow up a poster from A4 to A3, you want it to fit exactly – you don’t want to be cutting bits off!
The ISO standard for A4 size paper has dimensions of 297mm by 210mm. This ratio is or
which is close to
with
and
. This length/width ratio is approximately
for all sheets in the A series of paper.
Matt Parker, Standup Mathematician Talks About Paper Sizes
What Is the Best Approximation for the Square Root of 2?
A4 paper uses 99/70 as an approximation for the Square Root of 2. In fact, this is the most accurate approximation possible for which has a two digit denominator. If you use your calculator to work out the difference between
and the Square Root of 2 you will get 0.000072151 – that is a pretty accurate approximation for a simple fraction which can be remembered easily!
The Square Root of 2 as a Continued Fraction
A continued fraction is a special type of fraction, where the calculation goes on forever. We can express as the following continued fraction:
In fact any surd can be written as a continued fraction:
Continued fractions provide another way to approximate the value of the Square Root of 2.
What Is the Most Accurate Calculation of the Square Root of 2?
The current record stands at 10 trillion decimal places – knowing the Square Root of 2 to this level of detail serves no practical purpose – it is more a test of computing power and dedication. There will never be a shortage of people who want to break this kind of record – for Pi it has exceeded 30 trillion decimal places.
Square Root Day
Pi has its own special day which is widely celebrated on the 14th March (3.14 in the U.S. system). For Euler’s constant (e=2.718…) you can have a choice depending on which date format you want to follow – either marking it on the 7th February (7/2) or the 2nd July (2/7).
“Square Root of 2 Day”(1.42421…) doesn’t exist yet– but you could have a choice between the 4th January (4/1) and the 1st April (1/4) – April Fool’s Day! There are however days called ‘Square Root Days’ and these occur 9 times in each century on the following dates: 1/1/01, 2/2/04, 3/3/09, 4/4/16, 5/5/25, 6/6/36, 7/7/49, 8/8/64, 9/9/81. Can you spot the pattern?
How to Memorise the Square Root of 2 (Using a Mnemonic)
Here are some sentences to recall square roots (each to 3 decimal places):
The square root of 2:
” I wish I knew
( 1 . 4 1 4 )
the root of two “
The square root of 3:
” O charmed was he
( 1 . 7 3 2 )
to know the root of three “
The square root of 5:
” So now we strive
( 2 . 3 2 6 )
to know the root of five “
The square root of 6:
” We need more logistics
( 2 . 4 4 9 )
to know the root of six “
Mnemonics from: http://www.eudesign.com/mnems/_mnframe.htm
Related Content
Article by Hazel Lewis
Image Credits
Paper Size image Sven CC BY-SA 3.0, via Wikimedia Commons






