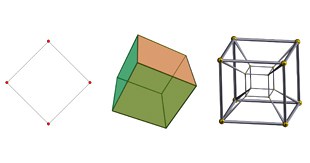
We live in a three-dimensional world, where the familiar directions of left-right, backward-forward, and up-down dictate everything that we see and experience. Three’s not enough for mathematicians though, as they can explore worlds of four, five, or even a million dimensions. These places are impossible to visualise, but that we can glimpse them with the power of numbers.
As you know, coordinates are numbers that pin down a point in space, and we use the coordinates (x, y, z) to find points in three dimensions. These coordinates tell us to start at the origin and then move x steps right, y steps forward, and z steps up. But what if we add another number, w, so that (x, y, z, w) specifies a point in four-dimensional space? We seem to have run out of directions to move in, so is this even possible? If you want to find your way to the fourth dimension, it helps to take a detour to the second.
Stick around
 Imagine that instead of living in our regular three dimensional world, you’re a stick figure inhabiting a sheet of paper. You can walk left and right or jump up and crouch down, but you can’t move backwards or forwards to escape the page. You also only need two coordinates, (x,y), to specify any point in space. Welcome to two dimensions.
Imagine that instead of living in our regular three dimensional world, you’re a stick figure inhabiting a sheet of paper. You can walk left and right or jump up and crouch down, but you can’t move backwards or forwards to escape the page. You also only need two coordinates, (x,y), to specify any point in space. Welcome to two dimensions.
As a two-dimensional being, you find it hard to picture the third dimension, because there doesn’t seem to be any extra directions you can move in. One day, you notice a speck of dust has appeared from nowhere. It expands into a circle that continues to grow. As you watch, amazed by this strange sight, the circle begins to shrink again, eventually returning to a speck of dust before disappearing all together.
You’ve just had a close encounter of the spherical kind. The growing and shrinking circles were actually a sphere passing through your sheet of paper. Your two-dimensional eyes can’t see the entire sphere, because they can’t access the third dimension, but the circular slices give an idea of what it looks like.
Use the forth
 It’s time to leave this paper world and return to three dimensions, but don’t forget what you’ve learnt during your time as a stick figure. Although we can’t view true four-dimensional shapes, three-dimensional “slices” can give an impression of what they look like. What would happen if a four-dimensional sphere, called a hypersphere, passed though our world? Instead of growing and shrinking circles, you’d see growing and shrinking spheres. It’s very hard for us to visualise how these spheres are all parts of the same shape though, as our three-dimensional brains just can’t handle it.
It’s time to leave this paper world and return to three dimensions, but don’t forget what you’ve learnt during your time as a stick figure. Although we can’t view true four-dimensional shapes, three-dimensional “slices” can give an impression of what they look like. What would happen if a four-dimensional sphere, called a hypersphere, passed though our world? Instead of growing and shrinking circles, you’d see growing and shrinking spheres. It’s very hard for us to visualise how these spheres are all parts of the same shape though, as our three-dimensional brains just can’t handle it.
Maybe it’s easier just to stick with numbers. A circle centred at the origin with radius r is described by the equation x² + y² = r². You can use this equation to test whether a point in two-dimensional space is inside the circle by plugging in the coordinates (x, y). If x² + y² < r², then (x, y) is inside the circle, and if x² + y² > r², then (x, y) is outside. This also works for three dimensions. The equation for a sphere is x² + y² + z² = r², and you can test any point (x, y, z) by plugging in the numbers.
Unsurprisingly, we can do the same trick in four dimensions with the equation for a hypersphere, x² + y² + z² + w² = r². Even though you can’t see a hypersphere, maths can tell you what it looks like. But if hyperspheres and other four-dimensional shapes are impossible in the real world, what’s the point in studying them?
Higher maths
 It turns out that higher dimensions are very useful in physics, and can also help to understand large sets of data. You may have heard people say that time is the fourth dimension, but this is a bit different from the fourth space dimension described by the number w. We can only travel forwards in time, not backwards, so physicists say our universe has 3 + 1 dimensions. which they study with four-dimensional maths. Some complicated theories say there might be even more dimensions, but they’re tiny and impossible to detect.
It turns out that higher dimensions are very useful in physics, and can also help to understand large sets of data. You may have heard people say that time is the fourth dimension, but this is a bit different from the fourth space dimension described by the number w. We can only travel forwards in time, not backwards, so physicists say our universe has 3 + 1 dimensions. which they study with four-dimensional maths. Some complicated theories say there might be even more dimensions, but they’re tiny and impossible to detect.
This kind of advanced physics is pretty far-out, but you can actually find higher dimensions right here on Earth. We’re used to think of dimensions in terms of space (or sometimes time), but a dimension can actually be any independent variable needed to describe the state of an object.
For example, think about the results you’re hoping to get in your GCSEs, or your Standard Grades in Scotland. You can treat each subject as one dimension, with exam results being either high or low. If you’re taking 10 subjects then the results of all your exams mark a point in 10 dimensions, and you’re get good grades by reaching the highest points in this 10-dimensional space. How’s that for something to think about during revision?
Economists and other people who study large amounts of data do same thing, turning variables into dimensions that they can explore in higher-dimensional space. This lets them use the maths of geometry to understand their data, and see patterns that might not be immediately clear. We may live in a three-dimensional world, but that doesn’t mean we have to stay here!