Imagine you are a farmer who owns an orchard. One of your greatest fears is that blight spreads through your orchard, destroying your crops and ruining your livelihood.
You therefore want to know how best to plant your trees in order to minimise the chance of the blight taking over.
Mathematicians have modelled this problem by representing the orchard as a grid of dots, with each dot representing a tree.
Lines are then added according to the probability of blight spreading between the trees. If two dots are connected then that represents two trees affected by blight.
In the first diagram below, the probability of blight spreading is only ¼ and not that many trees end up affected by blight. On the other hand when the probability of blight spreading is ½ or ¾ then these diagrams show that the majority of trees are quickly infected.
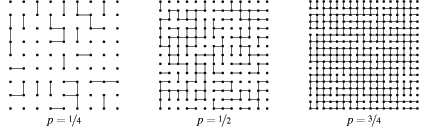
The mathematical study of problems like these is called percolation theory. Applications of percolation theory include the spread of flu, the prediction of earthquakes and even the formation of galaxies.
In percolation theory mathematicians are often studying infinite systems (imagine an orchard with infinitely many trees.) Mathematicians have discovered that in infinite systems there is something called the ‘critical probability’. The critical probability is the probability at which one tree becoming infected causes infinitely many trees to become infected.
In a square grid it has been shown that the critical probability is exactly ½. This means that if the probability of blight spreading is greater than ½ then infinitely many trees will become infected even if just one tree gets blight. If however the probability of blight spreading is less than 1/2 then only finitely many trees will become infected
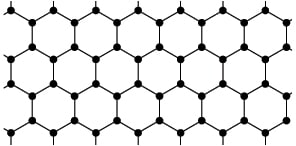
Honeycomb arrangement
Therefore it stands to reason that farmers will want to plant trees far enough apart so that the probability of blight spreading is less than ½ . If however trees are planted in a honeycomb arrangement then researchers have shown that the critical probability is 0.65 rather than ½ .
Even though the honeycomb arrangement doesn’t allow as many trees to be packed in as a traditional grid arrangement, the higher critical probability means that farmers can plant trees closer together.
If you are interested in finding out more about percolation theory then some undergraduate maths degrees include optional modules in the subject.
Article by Hazel Lewis
Adapted from a piece written by Colva Roney-Dougal and Vince Vatter in 50 Visions of Mathematics
Image credit: I, [GFDL, CC-BY-SA-3.0 or CC BY-SA 2.5-2.0-1.0], via Wikimedia Commons






