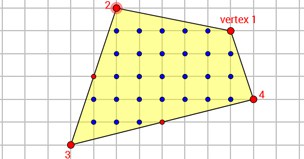
Pick’s theorem is one of those theorems in mathematics which seems too simple to be true. Take any polygon and lay it on a lattice. (A lattice is a grid of points where every point has whole number (integer) coordinates.) According to Pick’s Theorem all you need to do to find the area of a polygon is to count the points on the interior and on the boundary of the shape.
Pick’s Theorem then states that:
( stands for the number of points in the interior of the shape,
stands for the number of points on the boundary of the shape.)
Take the polygon below as an example. In this polygon and
. According to Pick’s Theorem,
which is the correct area of the polygon.
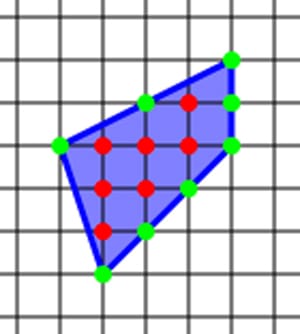
Pick’s Theorem does however only work for simple polygons – this means polygons which don’t intersect themselves and don’t have any holes, however it can be adapted to include holes.
Pick’s Theorem for polygons with holes
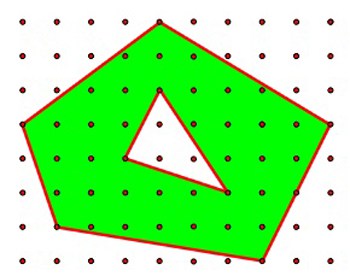
To use Pick’s Theorem on a shape like the one above you simply need to apply the theorem to the green shape without the hole and then subtract the area of the hole.
Area of Green shape (without hole) using Pick’s Theorem:
Area of the hole using Pick’s Theorem:
Total Area of the shape =
This approach can be expanded to a polygon with any number of holes. If you happen to be interested in the proof of Pick’s Theorem it is quite long but is not too hard to understand. A good explanation can be found here.
Equilateral Triangles
Pick’s Theorem can be used to show that you cannot draw an equilateral triangle on a lattice so that each vertex is on a grid point.
Imagine you have an equilateral triangle with base and height
. To work out the height in terms of the base we use Pythagoras’ Theorem:
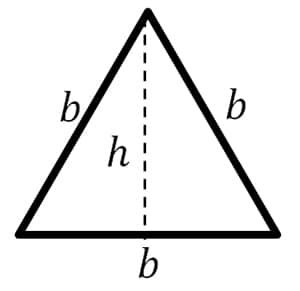
If we first calculate the area using the formula we get
.
If however we then suppose that we have drawn our equilateral triangle on the lattice points and that we want to use Pick’s Theorem, we would calculate that the . This will be what is called a rational number – it will either be a whole number or a fraction.
We do however now meet a problem, as must be what is called an irrational number. The reason for this is as follows:
must be a whole number as we have drawn our triangle on a lattice and
is an irrational number. An irrational number cannot be written as a whole number or a fraction. Therefore we have proved that we cannot draw an equilateral triangle on a lattice so that all its vertices touch lattice points.
Why not now try drawing some polygons and watch Pick’s Theorem calculate the area.
| This is an example of what is called proof by contradiction. We assume that we can draw an equilateral triangle on a set of three lattice points. We then show that this leads to a contradiction – i.e. Pick’s Theorem would imply that a rational number could be equal to an irrational number which is an impossibility. Therefore it must be impossible to draw an equilateral triangle on a lattice where all the vertices of the triangle are on a lattice. |
Article by Hazel Lewis