Pythagoras Saves the Whales

Whales Are Under Threat

A major threat to whales arises from them coming too close to shipping. This can lead to collisions between the ship and the whale, where the whale always comes off worse. Another threat arises if the ship is looking for oil and is using seismic signals. In this case the ship will detonate a small explosion and measure the echoes. This is a good way to find oil, but the explosions can injure any nearby whale. Fortunately, these two risks can be reduced by the use of mathematical modelling.

How Many Whales Are There?

One area in which maths can make a significant difference, is the seemingly simple one of telling us how many whales there are in the first place. Good conservation and management require an understanding of the status of the whale populations. A key component of this is an estimate of both the present population, and also the changes in the population resulting from the impact of different types of threat.

Simple, you say, let’s go out and count them! However, estimating the abundance of animals that are not particularly common, and which also spend most of their time below the surface is difficult. To estimate the population numbers, it is therefore necessary to use statistical methods and a good way to do this mathematically is to use the mark and recapture technique. In this method a (small) portion of the population is either captured, marked, and released or is observed for significant features (such as fin types for whales). Sometime later, another portion is captured/observed and the number of originally marked/identified individuals within this group is counted. In a well-mixed population, the number of identified individuals in the second group is proportional to the number of marked individuals in the whole population. Hence an estimate of the total population size can be obtained by dividing the number of identified individuals by the proportion of marked individuals in the second sample. For example, if 100 originals are originally identified, and in the second sample there are 5% of these, then the total population is estimated to be 20*100=2000 [1].

Ship Strikes

One major threat to whales, is being struck by a ship. For some populations, such as the North Atlantic right whale whose main habitat is the busy waters off the east coast of the USA and Canada, the mortality rate is particularly high compared to the overall population size. It is thought that mortality due to ship strikes may make the difference between extinction and survival for this species. The most effective way to reduce collision risk is to keep whales and ships apart. However, to do this we must know where the whales are, and in particular, how far the ship is from the whale. Mathematical modelling gives us a good way to do this.

Pythagoras’ Theorem Saves the Whales

If anyone is asked to name a theorem, then chances are that they will mention Pythagoras’ theorem. This states that for any right-angled triangle we have $a^{2}+b^{2}=c^{2}$ , as illustrated below.

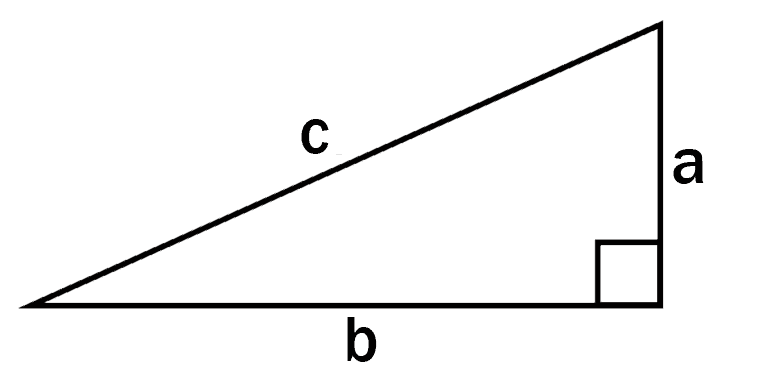
The reason that Pythagoras’ theorem is so useful to us in finding whales is that it can be used to estimate distances in general, and the distance of a whale from the ship, in particular.

To make sure that a ship does not hit a whale it has to be a certain distance from what is called the ‘mitigation zone’. Provided that the whale is outside the mitigation zone then it will be safe. The mitigation zone varies from ship and from whale to whale, but a distance of 400m is not unreasonable. Thus, to save the whales from ship strikes, or from surveying explosions, we must make sure that we can estimate the distance from them, so that they are outside the mitigation zone.

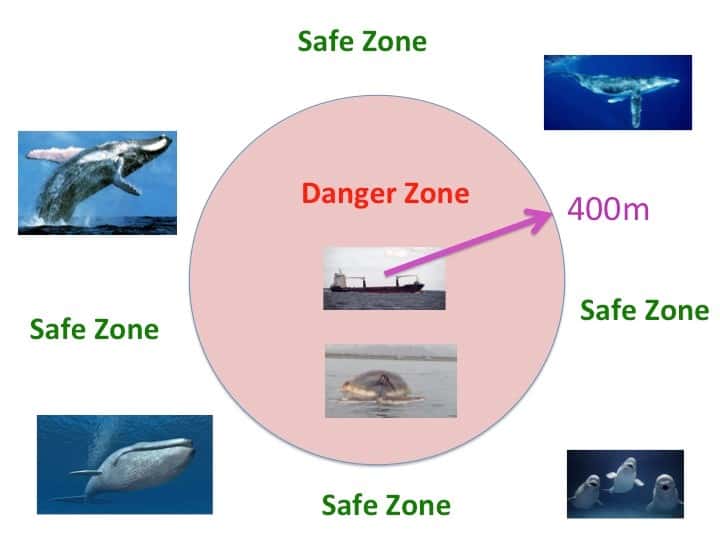safe zone whales We must now work out a way of finding the distance from the whale to the ship and to do this we combine physics with mathematical modelling. There are many ways to find out how far a whale is from a ship. The simplest of these is to spot it visually, and seismology prospecting ships have to carry ‘whale spotters’ as a result. Other techniques such as radar are less effective due to the relatively small size of the whale and its tendency to submerge. Active sonar is often used to detect fish (and submarines) and involves sending pulses of high energy sound which reflect off nearby objects. Detecting these reflections allows the location of the fish (or submarine) to be determined. However, active sonar must be avoided when searching for whales as it damages their own very sensitive navigation system and can lead them to beach and then to die.

The best way by far to detect the whale is simply to listen to it. Whales ‘sing’ and we can detect the sounds that they make. A spectrograph of a typical sound is shown below.

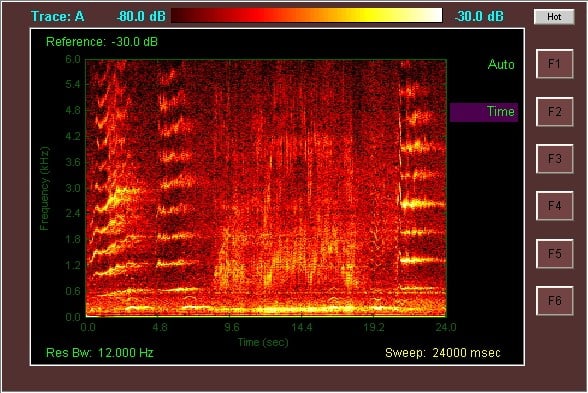
whales spectrograph
In principle by hearing when the sounds arrive, we can work out how far away the whale is.

But to do this we must use an approximate mathematical model. Our first step, as advertised above, is to look at the data. The pressure u of the detected sounds from the whale as they arrive look like this.

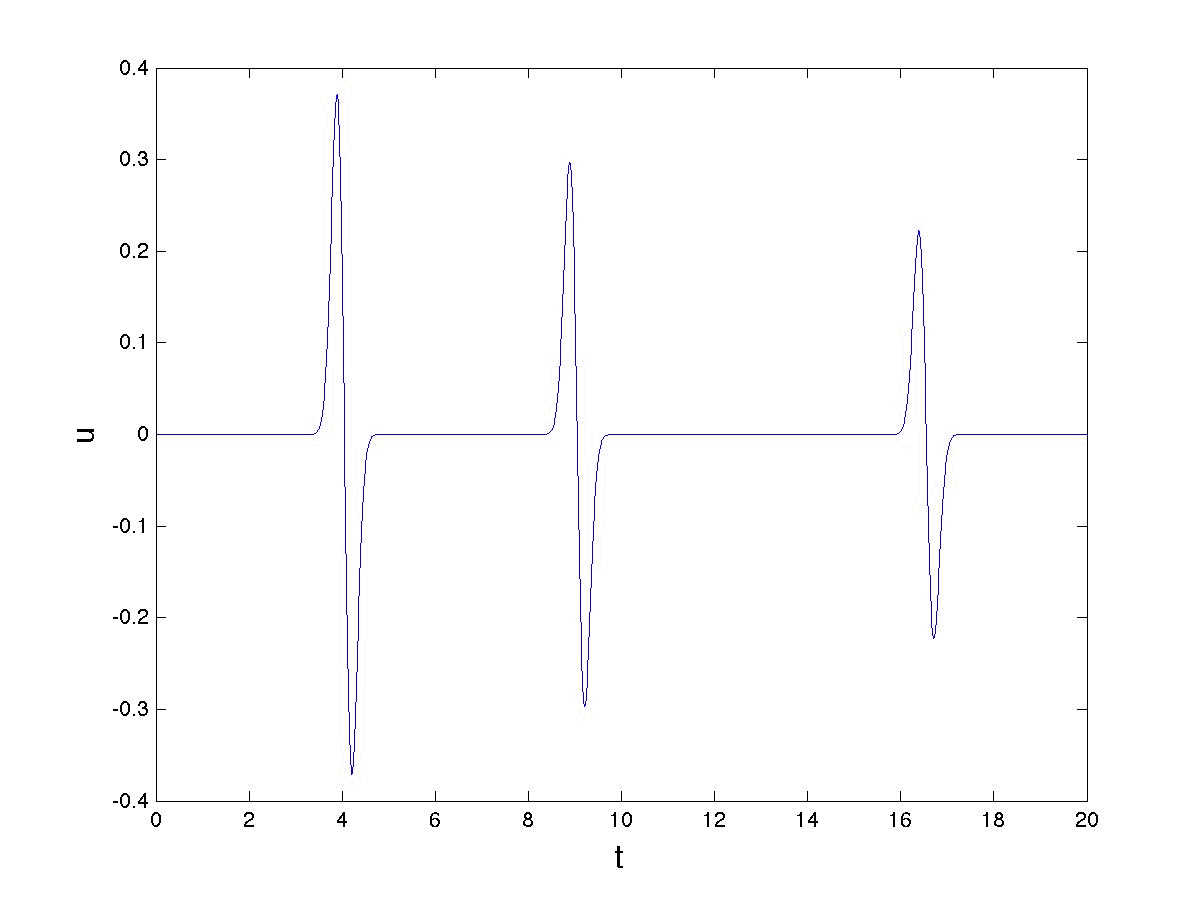To interpret this picture, we must next consider the physical situation. This is illustrated below. The whale is a distance L from the ship. We also assume that it is just underneath the surface of the sea, and that the sea has a (constant) depth of H. Using this we can interpret the graph of the detected sounds.

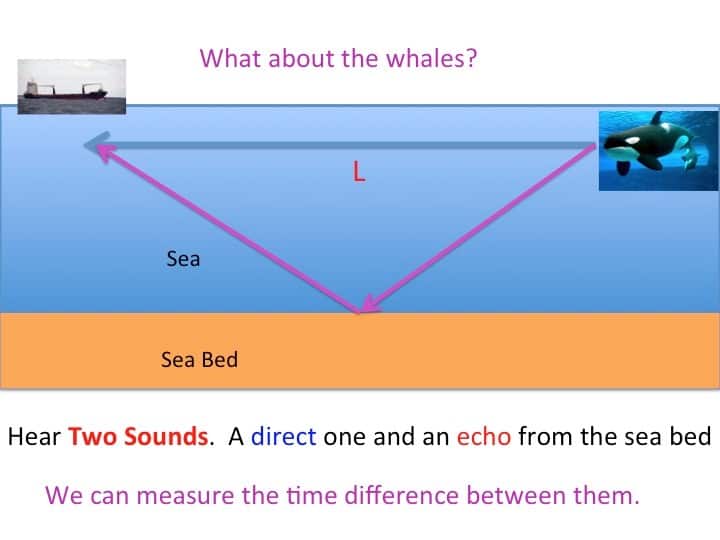What we are seeing here (at t=4) is the sound from the whale, followed shortly afterwards by the same sound reflected from the sea surface. Later (at t=8.5) we see the sound reflected from the sea bed followed closely by one reflected from the sea surface. Later still (at t=16) we see the sound reflected twice from the sea bed. The further they have to travel, the longer the sounds take to arrive, and the weaker they are when they do arrive.

We can now work out how long it takes the different sounds from the whale to arrive using mathematics. If the whale is a distance L away from the boat then the time of arrival of a direct sound from the whale to the boat is given by:

$t_{1}=\frac{L}{c}$

Here c is the speed of sound in water which is approximately 1500 metres per second.

If we knew when the whale emitted this sound then we could find L directly from this formula. However, we do not know this. To find the whale we must listen for the echo of this first sound, which will arrive a bit later as it has to travel a greater distance. If we suppose that the depth of the ocean is H and the distance travelled by the sound (on its straight-line path) is 2S then we can find S by drawing a couple of right-angled triangles and applying Pythagoras’ Theorem (as advertised earlier) as follows:

The total distance 2S is then given by: 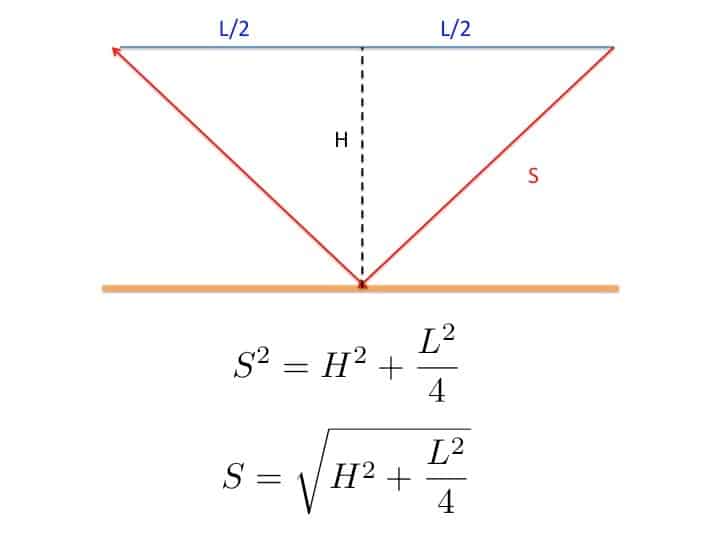$2 S=2 \sqrt{H^{2}+\frac{L^{2}}{4}}=\sqrt{4 H^{2}+L^{2}}$

The arrival time of the echo is then given by: $t_{2}=\frac{\sqrt{4 H^{2}+L^{2}}}{C}$

The resulting times for the pulses are then as shown in the figure below.

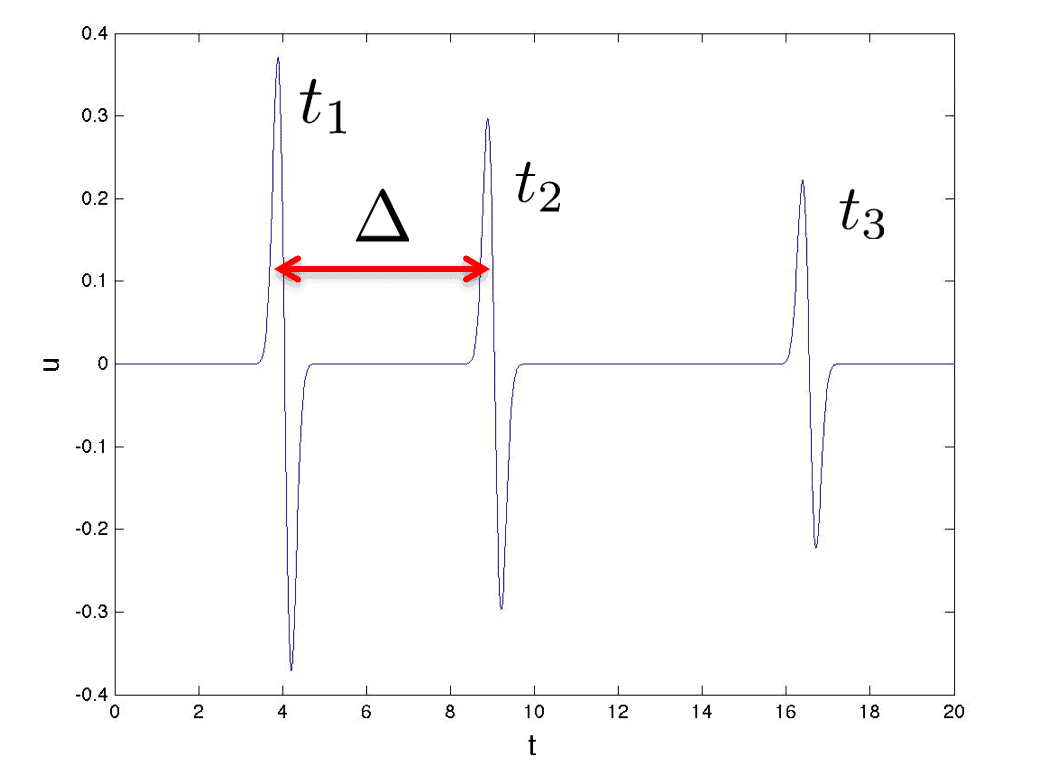Now, whilst we can’t tell when the sound of the whale was made, we can measure the time difference between the echo and the direct signal. This is given by: $\Delta=t_{2}-t_{1}$

So that $\Delta=\frac{\sqrt{4 H^{2}+L^{2}}}{C}-\frac{L}{C}$

Now for the clever bit. Knowing this time difference, we can work out the value of L and thus find out how far away the whale is. To do this we square the equation above to give $\Delta^{2}+2 \Delta \frac{L}{C}+\frac{L^{2}}{C^{2}}=\frac{4 H^{2}+L^{2}}{C^{2}}$

Cancelling the same terms from each side and rearranging we get $L=\frac{2 H^{2}}{\Delta C}-\frac{\Delta C}{2}$

Provided that we know H then we can find L, and hence find the whale. Here is an example of doing this when H = 100m is given below. In this we can see that if the time difference is less than 30ms then the whale is safe, but if it is longer than 30ms then the whale is in trouble. By means of this simple formula we can thus save the whales.

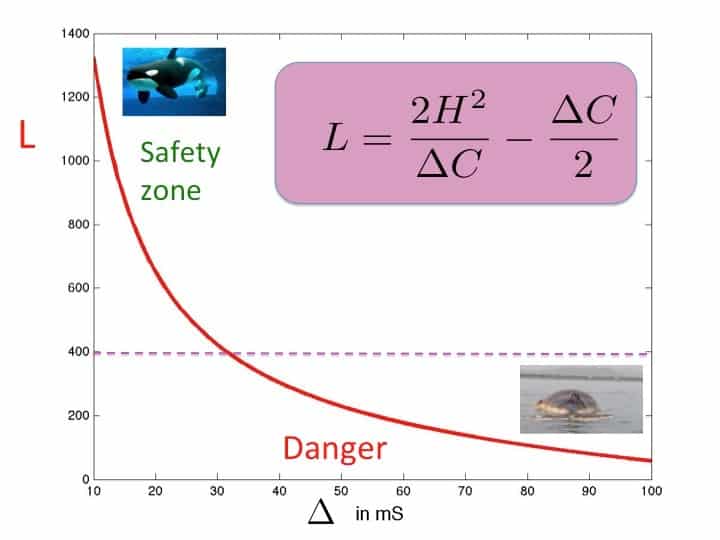Of course, as with all models we have made many simplifications and assumptions to get to this result. One of these is the assumption that we know the sea depth H. One way to find this, which is commonly used, is to employ active sonar. However, this, as we have seen, can injure the whales. A much better way is to make use of the other echoes from the sea-bed. By listening to these it is possible not only to locate the whale, but to also find H and much more besides.

This article was written by Professor Chris Budd OBE, University of Bath

References

[1] The mark and recapture method is described in https://en.wikipedia.org/wiki/Mark_and_recapture

Further Material

Full 58 minute Gresham Lecture on YouTube – Can Maths Save The Whales and Cure Cancer? By Chris Budd

Photo by Todd Cravens on Unsplash

Tags:

Pythagoras Saves the Whales

Whales Are Under Threat

How Many Whales Are There?

Ship Strikes