The best selling toy of all time is the Rubik’s cube. Easy to scramble, difficult to solve, many people think those who can complete the brightly coloured Hungarian invention are very clever.
Rubik’s Cube looks pretty simple: a cube with each face a different colour, split up into 27 smaller cubes. The smaller cubes – ‘cubies’ to Rubik’s enthusiasts – rotate and get shuffled around so the sides are no longer one colour. The challenge is to ‘solve’ the cube so the faces are solid colours again. But moving a cubie to a different location can need a series of rotations, and moving it to the right place can mess up any work you’ve done before.
There are 3,252,003,274,489,856,000 (say it ‘three and a quarter quintillion’) different possible positions for a Rubik’s cube, and only one ‘correct’ solution.
Learning the moves
A first step towards solving a Rubik’s cube is to understand the different ways it can move. The professor of architecture who designed it wanted to help his students understand movement in space and how objects relate to each other. Spotting which bits of a problem are already solved, and what your options are for swapping things around to do the rest, is a key maths skill and may explain why mathematicians are often good at the cube.
The centre squares of each of the 3×3 faces are fixed: they can’t move in relation to each other. For example, the white side is always going to be opposite the blue side. This tells you which colour each face will be when it is solved. Around this central 3D cross, slices can be rotated. The cube has no ‘right way up’, so these layers might be horizontal or vertical. Combining horizontal and vertical turns allows a cubie to be moved anywhere around the cube.
Following the recipe
People attempting to solve the cube have developed algorithms to do things like swap two edge pieces or rotate the position of three corner cubies. An algorithm is a set of simple instructions, like a recipe, to produce a result. They are the essence of programming and decision mathematics.
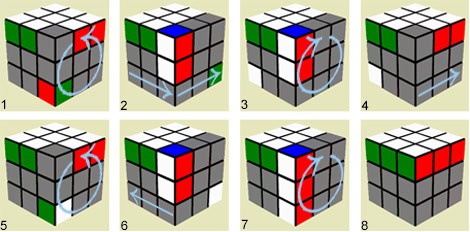
For example, suppose the puzzler has familiarised herself with how the puzzle can move, and is able to assemble one face in a solid colour, except for one corner. A 7-stage algorithm can be used to swap two corner pieces, as described below and shown in diagram form.
Prepare the cube by rotating it so the two corners you want to swap are on the right hand side of the front face (as in Image 1)
- Rotate the right hand face 90 degrees counter clockwise (Image 2)
- Rotate the bottom face 180 degrees (Image 3)
- Rotate the right hand face 90 degrees clockwise, (Image 4)
- Rotate the bottom face 90 degrees clockwise (as looked at from below) (Image 5)
- Rotate the right hand face 90 degrees counter clockwise (Image 6)
- Rotate the bottom face 90 degrees counter clockwise (as looked at from below) (Image 7)
- Rotate the right hand face 90 degrees clockwise (Image 8)
High speed racing
Frequent cubers will have many algorithms memorized for different arrangements. Combining these with an overall strategy – often solving a layer at a time, or starting from one corner – they can solve any of the quintillions (1,000,000,000,000,000,000s) of arrangements possible. Some can do this very fast indeed: ‘speed cubers’ typically take under 10 seconds. However, this speed is achieved by performing each rotation and flick very quickly, rather than finding the solution which takes the smallest number of moves.
Supercomputer solution
Since the release of the toy people have debated the minimum number of steps required to solve any configuration. This speculation continued until a team provided a definitive answer in 2010. Using a supercomputer, and exploiting symmetries between different arrangements – some of which are exactly the same, but with yellow, say, swapped with red – they produced a definitive mathematical proof. No matter how the cube is scrambled, 20 moves are all that are needed to return the cube to perfect solid colours.
Solving the Rubik’s Cube, like doing maths, can be thought of as something for brainy people. But the similarities don’t stop there. Both need you to understand the problem, and then follow a set of instructions you’ve learnt to solve it a bit at a time. If you keep going with it, you will find a satisfying solution easier than you think. As with a lot of mathematics, perseverance pays!
This article is based on a suggestion by Maddie White at St Georges College, Surrey, who won the Maths Careers Articles Competition (11-14 age group).