Imagine you have a pile of identical block shaped objects – they could be made of wood, or they could be as thin as rectangular playing cards. It’s easy to stack them directly on top of each other – if on the other hand you want to create an overhang then you might well guess that you won’t get very far. Surprisingly, if you sit down and work out the maths involved, then you will be amazed to find that you can keep stacking the blocks outwards forever – working towards an infinite overhang! This is what is known as the Infinite Block Stacking Problem, sometimes called the Leaning Tower of Lire.

How can the stack have an infinite overhang?
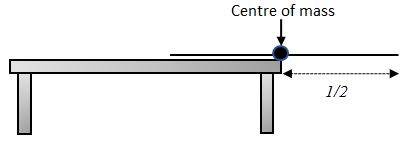
If you just have one block, then the centre of mass is exactly in the middle and you can balance your block or card to create an overhang which is half the length of the block.
Possible overhang with one block
Possible overhang with two blocks
Now take two identical blocks. A second block can balance on top of a first block, with an overhang of ½ just like it did with the table. We now need to know how big the overhang will be for the block resting on the table (call this x).
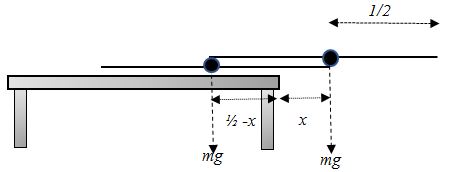
Using moments
Clockwise moment about end of table:
Anticlockwise moment about end of table:
Equate moments:
Hence so
This means that the total possible overhang for two blocks is , which means an overhang of
of a block.
Possible overhang with three blocks
Mark the balance point of two blocks:
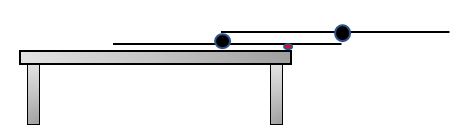
Replace the two blocks by a single equivalent:
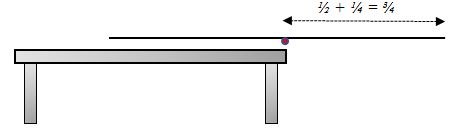
Put the single equivalent on top of a third:
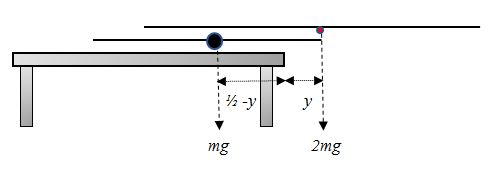
Using moments
Clockwise moment about end of table:
Anticlockwise moment about end of table:
Equate moments:
Hence: so
Replace the single equivalent by its original two:
This means that the total possible overhang for three blocks is , which is nearly a whole block.
Possible overhang with more than three blocks
If you continue the same process you will find that for n blocks, the total possible overhang is
What will happen as n becomes very large? Can we keep stacking blocks outwards from the table forever?
Luckily for us, the series is very famous and is called the Harmonic Series.
In the 14th Century Nicole Oresme proved that this series diverges, which means that as n tends towards infinity, the series does not have a finite limit.
In other words the stack of blocks will keep extending further and further out from the table forever!
The catch
Unfortunately the Harmonic Series diverges very slowly. This means that you will need a lot of blocks to get anywhere. Even if you use 1 million blocks, you will still only be able to extend beyond your table edge by the length of 14 blocks. However, just 10 blocks will allow you to extend beyond your table edge by about the length of 3 blocks, which could look very impressive (if you can practise enough to achieve this)!
The practical test
Now it is time to have a go yourself – take some playing cards and see how far you can get. Alternatively you can watch other people trying on YouTube.






