An ancient legend about some rice and a chessboard goes as follows:
“A wise old ruler wanted to reward his servant for an act of extraordinary bravery. The servant said:
‘Master I ask you for just one thing. Take your chessboard and place on the first square one grain of rice. On the first day I will take this grain home to feed my family. On the second day place on the second square 2 grains for me to take home. On the third day cover the third square with four grains for me to take. Each day double the number of grains you give me until you have placed rice on every square of the chessboard. Then my reward will be complete.’
The wise old ruler replied:
‘This sounds like a small price to pay for your act of incredible bravery, I will ask my servants to do as you ask immediately.’
Was the wise ruler wise after all?
The rice and chessboard legend has been repeated many times and in lots of different formats. In fact, some people trace the legend back to India where chess was invented. Was it a sensible reward, or did the wise ruler choose a course of action which would bankrupt his kingdom?
There are 64 squares on a chessboard. Let’s look at what would happen in the first week:
| Day | Grains placed that day | Total grains placed so far | Total Weight (Kg) | ‘Money’ earnt assuming 1kg of rice worth £1.20 |
| 1 | 1 | 1 | 0.000029 | £0.000035 |
| 2 | 2 | 3 | 0.000087 | £0.000104 |
| 3 | 4 | 7 | 0.000203 | £0.000244 |
| 4 | 8 | 15 | 0.000435 | £0.000522 |
| 5 | 16 | 31 | 0.000899 | £0.001079 |
| 6 | 32 | 63 | 0.001827 | £0.002192 |
| 7 | 64 | 127 | 0.003683 | £0.004420 |
So far, the reward is not looking so promising, and after 15 days the servant has only collected around 1 kg of rice.
| Day | Grains placed that day | Total grains placed so far | Total Weight (Kg) | ‘Money’ earnt assuming 1kg of rice worth £1.20 |
| 15 | 16384 | 32767 | 0.950 | £1.14 |
Let’s have a look at what happens on day 16-30. The situation starts to look a lot more positive for the servant.
| Day | Grains placed that day | Total grains placed so far | Total Weight (Kg) (rounded to 1 decimal place) | ‘Money’ earnt assuming 1kg of rice worth £1.20 |
| 16 | 32768 | 65535 | 1.9 | £2.28 |
| 17 | 65536 | 131071 | 3.8 | £4.56 |
| 18 | 131072 | 262143 | 7.6 | £9.12 |
| 19 | 262144 | 524287 | 15.2 | £18.24 |
| 20 | 524288 | 1048575 | 30.4 | £36.49 |
| 21 | 1048576 | 2097151 | 60.8 | £72.98 |
| 22 | 2097152 | 4194303 | 121.6 | £145.96 |
| 23 | 4194304 | 8388607 | 243.3 | £291.92 |
| 24 | 8388608 | 16777215 | 486.5 | £583.84 |
| 25 | 16777216 | 33554431 | 973.1 | £1,167.69 |
| 26 | 33554432 | 67108863 | 1946.2 | £2,335.38 |
| 27 | 67108864 | 134217727 | 3892.3 | £4,670.77 |
| 28 | 134217728 | 268435455 | 7784.6 | £9,341.55 |
| 29 | 268435456 | 536870911 | 15569.3 | £18,683.10 |
| 30 | 536870912 | 1073741823 | 31138.5 | £37,366.21 |
After 1 month or 30 days, the servant has earned a good salary. The problem with doubling is that the servant is about to get rich – very fast.
By day 36, the servant has earned the kind of money a Premier League Footballer would earn in a year:
| Day | Grains placed that day | Total grains placed so far | Total Weight (Kg) | ‘Money’ earnt assuming 1kg of rice worth £1.20 |
| 36 | 34359738368 | 68719476735 | 1992865 | £2,391,437 |
Things are starting to get a lot worse for the wise ruler. In modern times annual world rice production is equal to around 500 million metric tonnes, which is 500 000 000 000 kg or 5 x 1011 kg.
On day 54, the servant is due to have collected a total of 5.22 x 1011 kg of rice, exceeding modern day annual worldwide rice production. In ancient times rice production was much less, meaning that the wise ruler had been outwitted by the servant long before this point.
Some legends suggest that the servant was executed for his cheeky request, whereas others state that they were promoted for their cunning.
The problem with doubling
What pattern can you spot when you look at the number of grains placed each day?
Number of grains placed on each day: 1,2,4,8,16,32,…
This type of sequence is called a ‘geometric sequence’. This means that you always multiply each term by the same number (a common ratio) in order to get to the next term. In this particular geometric sequence we are multiplying by 2 each time. The nth term of the above sequence is 2n .
Now let’s take a look at the total number of grains which have been placed, which means adding up all the previous terms of the geometric sequence.
Total number of grains placed by end of each day: 1,3,7,15,31,63,127,…
To find out the total number of grains on the nth day, we can work out: 2n -1
There are 64 squares on a chessboard. This means that you can work out the total number of grains placed on the last day as: 264 -1 = 18446744073709551615
If you look at a small snapshot of the graph of 2n -1 you can see just how fast it is growing:
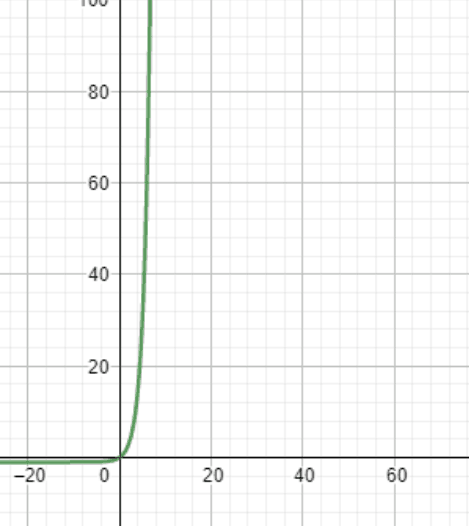
Whenever you have a sequence which involves doubling you need to be very wary indeed. The rice and the chessboard legend shows just how fast a sequence like this can grow.
This is why populations can’t continue to double in size for very long. In 1960 the world’s population was 3 billion, and by 1999 it had doubled to 6 billion. The earth has finite resources, meaning that this type of growth is not sustainable.
Pyramid Schemes – where doubling doesn’t work
A pyramid scheme is a get rich quick scheme which might be set up as follows:
Example Pyramid Scheme
You pay £100,000 to invest in ‘Flying Carpets LTD’ – a new company which is aiming to manufacture the world’s first fully functioning flying carpet.
All you need to do is to then recruit 6 new people who will all pay you £100,000 each. The six new recruits then need to recruit six more people each, and so on.
This seems to suggest that each person will get a guaranteed £500,000 profit!
Pyramid Schemes are illegal for a good reason. Look at how many people are needed at each level:
| Total number of people required: | |
| Level 1 | 1 person (probably the inventor of the scheme) |
| Level 2 | 1+6 = 7 |
| Level 3 | 1+6+36= 43 |
| Level 4 | 1+6+36+216 = 259 |
| Level 5 | 1+6+36+216+1296 = 1555 |
| Level 6 | 1+6+36+216+1296+7776 = 9331 |
| Level 7 | 1+6+36+216+1296+7776+46656 = 55987 |
The problems of the rice and the chessboard problem appear even more quickly when you are multiplying by 6 instead of 2. By Level 7, you need to find 46,656 recruits. It will be too hard to find so many people to invest and the scheme will collapse, leaving everyone at the previous level out of pocket by £100,000. Unfortunately pyramid schemes are usually hidden in lots of business speak which confuses investors and stops them from realising that they are investing in a scam.
Exponential Growth
Pyramid schemes and the rice and chessboard legend are examples of what is called exponential growth. This is where the total amount follows a rule such as y = ax, where a is a number. In the rice and chessboard legend a was equal to 2, whereas in most pyramid schemes a will be equal to a bigger number such as 6. Understanding the mathematics of exponential growth will help you understand lots of real world situations such as compound interest, and the growth of bacteria. (As well as helping you avoid falling for a scam.)
Image Credit:
Chessboard by Svjo [CC BY-SA 4.0], via Wikimedia Commons






