How is GCSE maths used in everyday life?
Here are 10 examples of where people use percentages in everyday life or in their careers. Whether you are hoping to work at NASA, or want to go out and buy your first house – percentages will be needed.
Please note: The maths careers website is a resource which is aimed at the whole of the United Kingdom, and any mention of GCSEs and A-levels can also be applied to equivalent qualifications in Scotland.
Weather Forecasting Probability
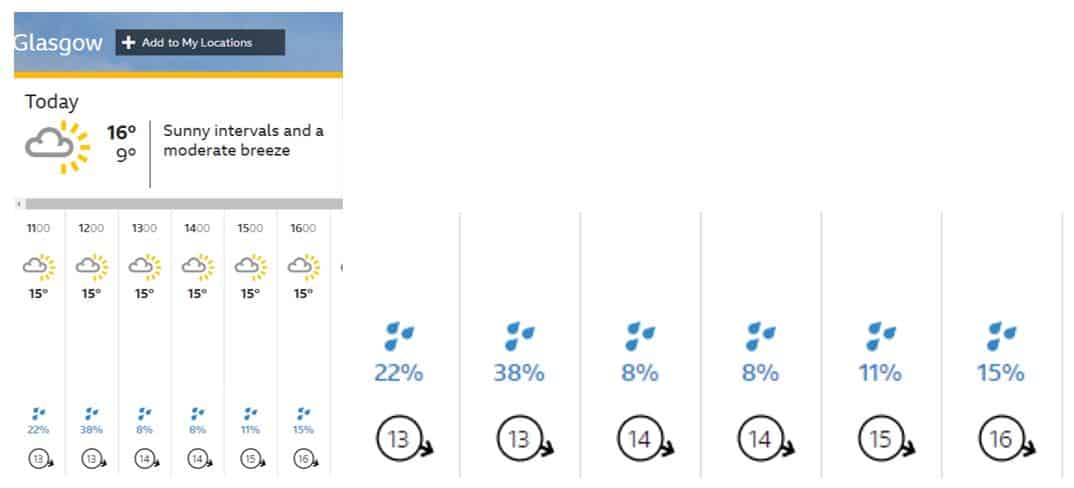
If you look at a weather forecast then it will show a percentage chance of rain, usually covering a one-hour time frame. This is based on the ‘Probability of Precipitation’ (POP) equation:
Probability of Precipitation =
If we think about a city like Glasgow, then C is the probability that it will rain somewhere in Glasgow in the next hour (C stands for confidence), and A is the percentage area where that rain will fall.

For example, if the forecasters think that there is a 50% chance of rain hitting Glasgow in the next hour and they also think that only 80% of the area of Glasgow will be rained on, then the Probability of Precipitation is 0.5 x 0.8 = 40%. It is important to look at the type of rain which is predicted – a 40% chance of light rain might not concern you, whereas a 40% chance of heavy rain is a different matter. In many real-life situations probabilities are often presented to the public as percentages.
YouTube Video explaining the Probability of Precipitation Equation further
How Many Red Skittles in a Packet? Manufacturing Percentages.

Do you have a favourite colour of sweet and do you find that they appear less often in the packet? One company set about testing this theory on a number of well know sweet brands, and found that different colours don’t appear evenly. For Skittles there are 5 colours which means that you would expect each colour to appear 20% of the time, whereas red sweets (the supposed favourite) were only found 15% of the time. The company which was investigating doesn’t share how many packets they analysed (meaning that we can’t rely on this research) but if they are right, then the manufacturers are releasing sweets in different percentage amounts.
This might seem like a trivial example; however, manufacturers use percentages all the time – for example in monitoring the cost of ingredients or reducing the percentage of rejected goods. Manufacturing is a tightly controlled process – someone making Skittles must know the secret truth – are there really less red Skittles?
Percentage Gradients on Roads

Do you think that 20% is quite a low percentage? Not when it comes to driving – a 20% gradient means that for every four steps forward you take, you will then take one step vertically upwards which means an angle of 14 degrees from working out . The 20% refers to the fact that you are walking vertically upwards for 20% of the time.
(What is confusing is that if we calculated the gradient of this line in a maths lesson we would get: )
Gradients that we are used to in maths lessons are not the same as percentage gradients. The authorities must feel that percentage gradients are easier to understand out on the road.)
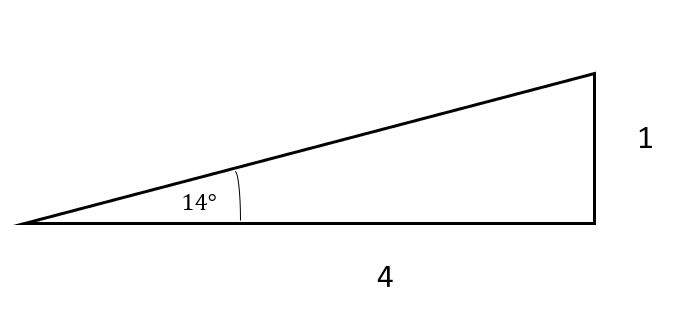
Before 1975 road signs used to be written as a ratio, with 20% being equal to a 1:5 ratio. You will still see some of these signs when you are out and about.

The steepest street in the UK is Ffordd Pen Llech in Harlech, Wales which has a gradient of 37.5%. This has been rounded to 40% by the Highways Agency in its signage.

Traffic Light Labels on Food
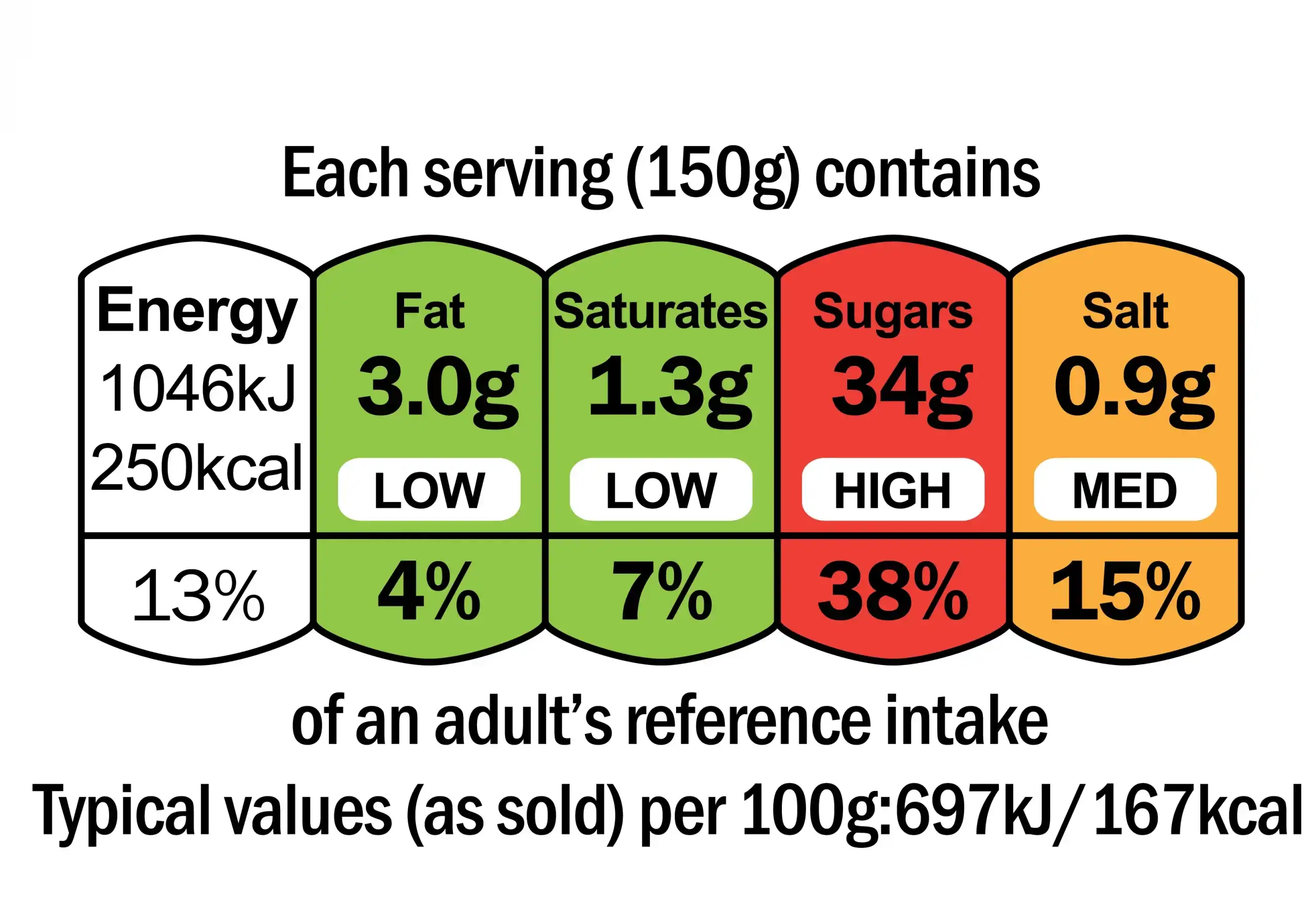
You can find traffic light labels on most food packets in the UK which include a percentage of the ‘reference intake.’ On a typical cream doughnut it might say 43% under saturated fat meaning that it contains 43% of the maximum amount of saturated fat an adult should eat in a day. If an adult is in a shop they can easily round this up in their head to 50% and understand that if they eat two cream doughnuts, they will have reached their recommended daily limit for saturated fat.
While these are only recommendations, and breaking them on one day won’t hurt, on balance they can help us to live more healthily. This is just one example of percentages helping people to stay healthy.

Percentage Vaccinated
In the Covid-19 pandemic, statistics are everywhere and one key measure is the percentage of a population which is vaccinated. Different countries have different sized populations, for example the population of the U.S. is four times bigger than that of the UK. It wouldn’t make sense to compare the total number of people vaccinated, instead it is much more useful to look at the percentage vaccinated.
With some diseases it also may be possible to achieve herd immunity if a high enough percentage of the population is vaccinated. If you take the childhood disease Polio, then 80-85% of the population needs to be vaccinated before herd immunity is achieved.
Unfortunately, herd immunity is currently looking unlikely for Covid-19, with one reason being the emergence of new variants of the virus. It is however important to remember that vaccines still protect individuals from death and serious disease, even if herd immunity is not achieved.
Inflation

Did you know that a pint of milk only cost 25p in 1990? Now you will need to pay more like 50p and by the time you read this article it may well have gone up again. What has happened is called inflation – since 1990 this pint of milk has doubled in price which has been caused by prices rising on average by 2% per year. A body called the Office for National Statistics looks at a typical ‘basket’ of goods each month and works out what percentage the goods have gone up by. This is called the Consumer Prices Index (CPI) which is a measure of inflation. If your trainers cost £50 in January and then £55 in February your trainers have gone up by . Inflation is critical to the economy and to daily spending power.
Biology – Osmosis

Percentages are everywhere in biology. One example is calculating percentage mass change in the process of ‘Osmosis’ where water diffuses across a membrane. This is a key concept in GCSE biology, and one which is used on a daily basis by many practising biologists.
GCSE Bitesize Maths – Calculating percentage gain and loss of mass in osmosis
Football – Ball Possession Percentage

From firing the current manager to repainting the stadium, football fans have got strongly held opinions on most things. The ball possession percentage is no different – some fans think it’s the key to glory whereas others think it hardly matters. Undoubtedly players, managers and pundits study this percentage carefully and it is just one of many football related percentages which have come to feel crucial to the beautiful game.
Ball possession used to be calculated by relying on someone starting and stopping a manual timer, whereas nowadays it is measured using video-based data. Find out more: Ball possession in football – how it’s calculated and how it matters
Plagiarism – Percentage Similarity

Cheating never pays – but unfortunately in the digital age some students can be tempted to borrow text from the internet or from other students, especially when they are working on an unsupervised piece of work such as coursework. This is why many organisations and universities are now using software packages such as Turnitin to check for a similarity percentage. In Turnitin each piece of work will be given a similarity percentage and organisations will then have a policy on what level of similarity is acceptable.
| Blue: No matching text |
| Green: One word to 24% matching text |
| Yellow: 25-49% matching text |
| Orange: 50-74% matching text |
| Red: 75-100% matching text |
Climate Change
Percentages are key to understanding climate change. For example by looking at which sectors or countries are generating the most emissions, decisions can be made on how to make reductions.
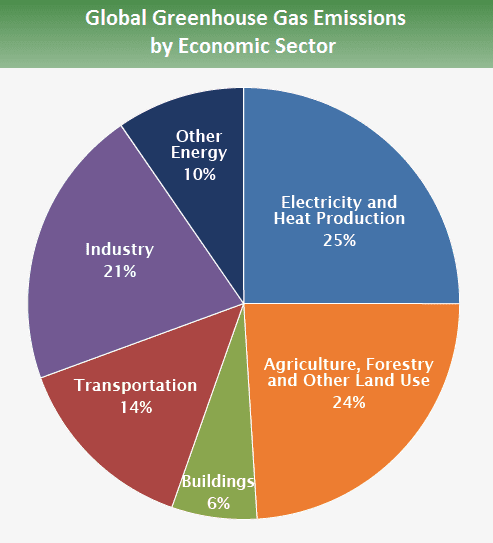
Source: https://www.ipcc.ch/report/ar5/wg3/ (2014)
Fractions, Decimals, Percentages and Ratios
Don’t forget that Fractions, Decimals, Percentages and Ratios are all connected – for example a percentage means parts out of 100, so that 65% is the same as 65/100. This means that a good understanding of percentages will enable you to understand situations which include decimals, fractions and ratios.
Article by Hazel Lewis






