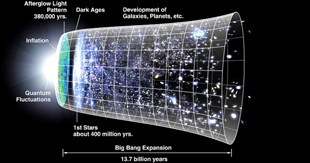
There was a time when the Earth was at the centre of the Universe, or so the planet’s then inhabitants thought. Now, not only do we know we are but one of eight planets orbiting the Sun, but the Sun is just one of around two hundred billion stars orbiting around a super-massive black hole at the centre of our Milky Way galaxy. In turn, the Milky Way is just one of around two hundred billion galaxies in the Universe. In fact, if you were to add up all the stars in the Universe they would outnumber the total number of heartbeats in humanity’s history by about a hundred to one.
However, even as late as the 1920s it was thought the Milky Way alone was the extent of the Universe. Then along came Edwin Hubble. He used stars called Cepheid variables to prove that two fuzzy patches in the sky were too far away to be in the Milky Way. Cepheid variables are stars that regularly vary in brightness and the period of this variation is tightly connected to the luminosity of the star – how much energy it emits per second.
The intensity of an astronomical object is the amount of that initial power that actually falls on an area of the Earth. So it’s the energy a telescope receives from that object per second per square metre.
The relationship between intensity and luminosity is:
where I is intensity, L is luminosity and D is the distance away from the object. Notice how the denominator is the surface area of a sphere – the object emits light equally in all directions and the light received by telescopes is a portion of that sphere.
 Knowing the luminosity of the Cepheid from its variation period, and measuring the intensity through his telescope, Hubble was able to calculate the distance to the Cepheid. By measuring the intensity of the wider galaxy it is in, and now knowing the distance to it, you can also estimate the luminosity of that whole galaxy using equation (1). Armed with a benchmark for the approximate luminosity of a galaxy, you can then start to work out the approximate distance to other galaxies that are too far away to pick out individual Cepheid variables.
Knowing the luminosity of the Cepheid from its variation period, and measuring the intensity through his telescope, Hubble was able to calculate the distance to the Cepheid. By measuring the intensity of the wider galaxy it is in, and now knowing the distance to it, you can also estimate the luminosity of that whole galaxy using equation (1). Armed with a benchmark for the approximate luminosity of a galaxy, you can then start to work out the approximate distance to other galaxies that are too far away to pick out individual Cepheid variables.
In doing so, Hubble noticed that the galaxies he was observing seemed to be moving away from us. He proved this using the Doppler effect. When an object is moving towards you it squashes the wave of light (or sound) together. Now with a smaller wavelength – a higher frequency – a light wave appears more blue. It is said to have been blue-shifted. Oppositely, if an object is moving away from you, it drags the wave out – the wavelength goes up and the frequency goes down. The object appears redder (red-shifted).
Equation (2) quantifies the Doppler effect
where v is the velocity of the object, c is the velocity of the medium (i.e. the speed of light), ? is the telescope-observed wavelength and ?0 is the laboratory, or rest frame, wavelength.
The recession velocity is calculated by looking at the spectrum of the galaxy. It is known that certain elements emit or absorb light at very specific wavelengths in the lab here on Earth – these are used as the rest frame wavelengths. The same emission or absorption lines in the light from the galaxy are seen, but their observed wavelengths have been shifted due to the motion of the galaxy.
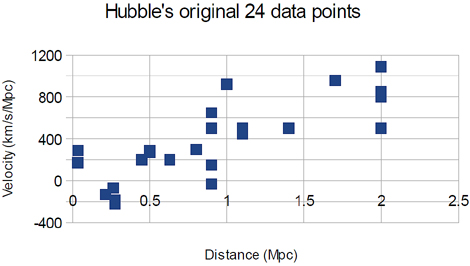
So Hubble now knew how far away each of his galaxies were and also how fast they were moving away. He plotted his results on a graph of velocity against distance. What he found overturned astronomy in an instant.
The points lie around a straight line with a positive gradient – the further away the galaxy, the faster it was moving away. The Universe was expanding. (Mpc is a megaparsec, a massive unit used to measure the vast distances in space)
If all the galaxies are moving apart now, yesterday they were closer together. A thousand years ago they were closer still. It is a natural consequence of an expanding universe that at a point long in the past the Universe began at a single point: the Big Bang. How long ago was it? The answer lies hidden in the graph.
From his findings Hubble knew the relationship between recession velocity and distance was linear.
This allowed him to formulate Hubble’s law:
where H0 is Hubble’s constant.
A straight line has the equation y = mx + c and so Hubble’s constant is simply the gradient of the graph. The most exquisite measurements from the Wilkinson Microwave Anisotropy Probe (WMAP), a space-based telescope, find that:
As both kilometres and megaparsecs are measures of distance, H0 has units of inverse time; the age of the Universe is simply the reciprocal of the gradient of the graph.
If we want only units of s-1 to remain, substituting in the number of kilometres in one megaparsec simultaneously eliminates both megaparsecs and kilometres from the units. There are 3.0857 x 1019 km in one megaparsec.
Then turning it all upside down gives the age of the Universe as:
Using the value of the Hubble constant from WMAP gives the age of the Universe as 4.40 × 1017 seconds. This can be converted into billions of years by dividing by 60 × 60 × 24 × 365.25 × 109 which yields an answer of ~ 13.87 billion years.
So our Universe was born just under 14,000 million years ago; the Earth is thought to be only 4540 million years old. Different ways of calculating the Hubble constant give slightly different values of the age of the Universe. However, most methods give a value of around 70 for the Hubble constant, consistently placing the Universe’s age at just shy of the 14 billion year mark.