Linear equations are the simplest kind of equations you come across in maths. You may be asked to solve a linear equation:
find x if 2x+7=31,
or to draw the graph of a linear equation such as y =2x+1, which is a straight line, or to solve simultaneous linear equations:
find x and y, where x+2y+3=8 and x+y=3.
We all solve linear equations in our heads all the time without even noticing it. If, for example, you have bought two CDs, for the same price, and a book, and know that you spent £20 pounds in total and that the book was £6, then you solve the linear equation 2x+6=20 to find out that the price of each CD was £7.
But the use of linear equations goes far beyond every-day problems like this one.
Computer graphics
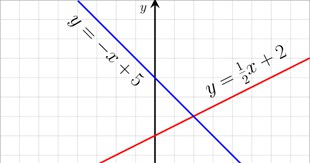
Computer graphics programmers use what is called “linear algebra”. As a simple example take the figure below. We can describe the location of each point on the image by a coordinate system. A point has co-ordinates (x,y) if you can get to it from the point where the two axes meet by taking x steps in the horizontal direction and y steps in the vertical direction. Now suppose you would like to rotate that image clockwise through a sixth of a turn. Then you can calculate that every point that previously had the co-ordinates (x,y) now moves to the position with co-ordinates
(0.5x + 0.866y, 0.5y-0.866x).
The two new coordinates have a similar form to the linear equations above and this is why graphics programmers end up having to solve a lot of linear equations.
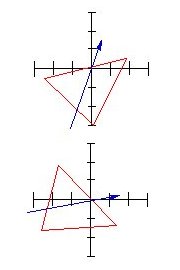 This is a simple example – you can imagine that if the images involved are a lot more complicated, for example three-dimensional, and if the object is to move in a much more complicated way, then the programmer must be able to handle a great number of simultaneous linear equations, involving many variables.
This is a simple example – you can imagine that if the images involved are a lot more complicated, for example three-dimensional, and if the object is to move in a much more complicated way, then the programmer must be able to handle a great number of simultaneous linear equations, involving many variables.
Economics
Economics is another area that makes use of linear equations a lot. Think, for example, of supply and demand. Your demand for a product – a chocolate bar or a car – will depend on the price of the product and how much you earn, among other things. If the product is very expensive, and you’re not that rich, you probably don’t want too much of it. If it’s cheap, like the chocolate bar, you may want a lot (unless you’re worried about your teeth). The demand is often expressed as linear equation:
D = a – bP +cI, where D is the demand, P the price and I your income. You can see that D goes down if P goes up (that is the reason for the minus sign), and it goes up as your income goes up. In a similar way, the supply can be expressed by a linear equation. Economists and other people in the financial world work with these kind of equations all the time.
The study of genes
Systems of linear equations also come up a lot in the study of genes. If you want to find out what a particular gene actually does, you have to see how it influences all the chemical processes in our body. There are hundreds of those going on in our bodies all the time, for example we produce sugars and proteins. The way these processes work, and how they influence each other, can be expressed by large systems of linear equations.
These are just three examples of how these equations are used in the real world. But there is another very important thing about them: they are the simplest equations there are. Equations are used in many areas to model the world around us. A biologist will use them to get an idea of how a population of animals might change over time. An economist or financial adviser will use them to predict the economy or the future profits of a company. An engineer will use them to work out the exact proportions of a building, like a bridge or a sky scraper, and how much and what kind of materials to use. In short, equations are a fact of life for many people, and to be able to work with them you need to start with the simplest ones – the linear equations.