Okunoshima Island in Japan is also known as Rabbit Island for a very good reason. It is inhabited by hundreds of wild rabbits which have been known to chase tourists and stampede around in large packs. The island has become a popular destination for tourists and there are lots of videos on YouTube showing the rabbits’ unusual behaviour. (For example look at this video)
Rabbit Island was used as a site for producing chemical weapons during the Second World War. It was subsequently abandoned due to health concerns, and no one is sure where the rabbits came from. One theory is that the rabbits escaped from being tested at the chemical weapons establishment, another theory suggests that rabbits were released by school children in the 1970s.
One thing for certain is that the rabbits have no predators on the island and that they can breed without any pesky foxes getting in their way.
 In 1202, Italian mathematician Fibonacci posed a mathematical rabbit problem. In his book Liber Abaci (The Book of Calculations) he wondered how many rabbits would be produced in perfect circumstances. (i.e. where there are no predators, just like on Rabbit Island!)
In 1202, Italian mathematician Fibonacci posed a mathematical rabbit problem. In his book Liber Abaci (The Book of Calculations) he wondered how many rabbits would be produced in perfect circumstances. (i.e. where there are no predators, just like on Rabbit Island!)
Fibonacci posed the theoretical problem as follows:
Imagine you have a pair of rabbits, one male and one female in a field. How many rabbits will they produce after one year?
Fibonacci made the following assumptions:
1. No rabbits die or are eaten by predators
2. Each female reproduces every month, starting from the second month that she is alive.
3. Every time the female reproduces she gives birth to one pair of rabbits – (one male and one female).
Let us look at how the number of rabbits grows:
| Start of Month | Number of pairs of rabbits | Total pairs of rabbits at start of the month |
| 1 | 1 pair (just the original pair) | 1 |
| 2 | There is still just one pair of rabbits at the start of the month. By the end of the month they have produced one more pair to make 2 pairs. | 1 |
| 3 | In this month only the original pair can breed making a total of 3 pairs by the end of the month. | 2 |
| 4 | In this month, the first two pairs can breed making a total of 3+2 = 5 pairs by the end of the month. | 3 |
| 5 | In this month the first three pairs can now breed making a total of 5+3 = 8 pairs by the end of the month. | 5 |
| 6 | In this month the first five pairs can now breed making a total of 8+5 = 8 pairs by the end of the month. | 8 |
It can be hard to take in what is happening and a diagram can be more helpful:
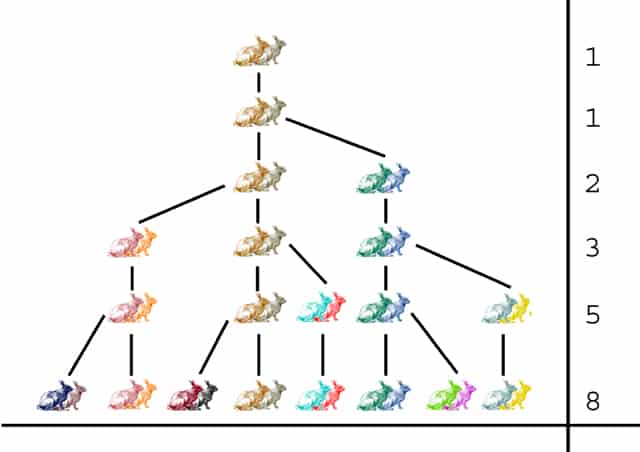
By now you may have spotted the sequence of Fibonacci numbers, one of the most famous sequences ever described: 1,1,2,3,5,8,13,21,…
Each number in the sequence is made by adding the two previous numbers together. We can continue the sequence until we have the first 13 Fibonacci numbers:
1,1,2,3,5,8,13,21, 34, 55, 89, 144, 233
At the beginning of the 13th month, (i.e. at the end of the year) we have 233 pairs of rabbits, which is 466 rabbits in total!

In reality rabbits have much bigger litters, with the average female having six babies each time she reproduces. This has led some people to estimate that a single female rabbit will have 184,597,433,860 descendants in just seven years. The situation is far worse than Fibonacci imagined.
This means the huge numbers of rabbits on Rabbit Island could easily have resulted from just a single pair of rabbits being released on the island. The reason that there are only millions and not billions of rabbits on the island is that the population will naturally be limited by space, disease, availability of food and other factors.
Fibonacci numbers also turned out to be very interesting in their own right, for example you can also read about them in ‘The Golden Ratio‘ article.
| Lots of mathematicians work in the field of population dynamics – looking at how populations might change over time. For example mathematicians study how fish populations are decreasing due to over fishing.
If you are interested in a career in this area, you should try and take A-level mathematics and Further Mathematics if you can, followed by a degree in mathematics, statistics or an environmental science. People usually specialise with postgraduate qualifications. |
Article by Hazel Lewis






