Every mathematician knows some problems are harder than others. Finding the prime factors of 1,005,973 will probably take you a while, but once you know that the answer is 997 and 1009, it’s easy to verify by multiplying them together. Wouldn’t life be so much simpler if solving a problem was as easy as checking the answer fits?
This might be possible, if P = NP. Don’t mistake this for an algebraic equation – P and NP refer to sets of problems, not variables. Understanding these sets can be difficult, but it’s worth persevering because P versus NP is one of the most fundamental questions in computer science. If you can prove that the two sets are the same (or even that they’re not) you’ll be in the running for one million dollars, and if you’re lucky, it could be six million.
What’s the problem?
Computers solve problems by running programs called algorithms, lists of instructions that specify each step involved. Different algorithms can be used to solve the same problem, but naturally we always want to use the one that gives the answer in the shortest possible time, so we need a way of comparing algorithm speeds. It’s not a question of how fast your computer is – a supercomputer will always beat a pocket calculator, no matter the algorithm – but how many calculations the algorithm requires. Suppose you need to find the largest value in a list of n numbers. The algorithm might go like this:
- Compare the first number to the second number, and keep the largest in memory.
- Compare the next number to the number in memory, and keep the largest.
- Repeat step 2 until you reach the end of the list. The number in memory will be the largest value.
This algorithm examines each number in turn and compares it to the largest, so the number of calculations involved will be proportional to n, the amount of numbers in the list. By comparison, a simple algorithm for multiplying two n-digit numbers requires about n2 calculations. Algorithms that take nx steps to finish are said to run in polynomial time, and thus belong to class P, but not all problems can be solved this quickly.
Not so fast
A famous example is the travelling salesman problem: given a list of n cities and the distances between them, can you find the shortest route that visits every city before returning to your starting point? A simple problem when you’ve only got a few cities, but the complexity quickly balloons as you add more stops to the route. The best algorithms require around 2n calculations to solve the problem, and thought the fastest computer in the world can do around 1015 calculations per second, it would still take 40 million years to come up with the best route for 100 cities.
Algorithms like this that need xn calculations are said to run in non-polynomial time, or non-P, and problems solved by non-P algorithms are generally considered to be hard. It’s difficult to prove that a problem is non-P though, because you would have to investigate every possible algorithm and show that none of them run in polynomial time – a pretty hard task in itself.
Check your answer
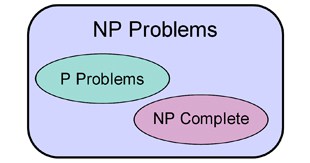
What we do know is that many non-P problems can be verified in polynomial time. These kinds of problems are said to run in non-deterministic polynomial time, and belong to class NP. It may be practically impossible to find a solution to an NP problem but if you happen to have an answer, it’s easily verified. Calculating the prime factors of a number is a typical NP problem, as demonstrated in the introduction.
It turns out that many NP problems are equivalent: if you have a polynomial time algorithm for one of them, it can be adapted to solve any NP problem. This group of problems, which includes the travelling salesman problem, are called NP-complete. A polynomial time algorithm for an NP-complete problem would instantly prove that P = NP, because it could be adapted to solve any NP problem, but how likely is it that we’ll ever find one?
The big question
The Clay Mathematics Institute have chosen P versus NP as one of their seven Millennium Problems, some of the most difficult and important in mathematics. The solution to each is valued at one million dollars, but depending on the answer, solving P versus NP could net you the lot.
Most mathematicians and computer scientists believe that P probably doesn’t equal NP. There are over 3000 known NP-complete problems, but we’ve yet to find a single polynomial time algorithm to solve one, so it seems unlikely that we ever will. A more intuitive argument suggests that verifying an answer is a very different task to finding one in the first place, so it would be strange to prove they are actually equivalent. But what if P really does equal NP?
The consequences depend on the proof. It may be possible to show that P = NP without producing a polynomial time algorithm for an NP-complete problem, in which case we still wouldn’t know how to easily solve NP problems. If the proof did lead to an algorithm however, the world would be transformed. The security of online transactions and other cryptographic communications rely on NP problems, so such an algorithm would make encrypted messages impossible. On the plus side, computers would become much more powerful, and businesses could increase their efficiency with perfect solutions to logistical problems such as the travelling salesman.
Perhaps most importantly, maths would never be the same again. Mathematical proofs can be translated into code that a computer can read through, line by line, to confirm whether they are correct. If you had an algorithm that proved P = NP, it would mean a computer could find a proof for any theorem, including the six other Millennium problems. One, the Poincaré Conjecture, has already been solved, but that still leaves you with six million dollars – not to mention the admiration of mathematicians world wide. Is it any wonder then that proving P = NP is a very, very hard problem?