The first time I saw a chocolate fountain in action was at a wedding fair. I was instantly fascinated by the inward–falling sheets of chocolate. Why doesn’t the chocolate fall straight downwards? I even got the owner of the stall to turn the fountain off and on again so I could see the startup: the chocolate does fall inwards even before it’s reached the bottom.
That got me thinking about the chocolate fountain as a whole. I’m a specialist in non–Newtonian fluid mechanics– that is, the flow of fluids that are in some way not as simple as air, water, or syrup. There are many ways a material can deviate from the simple model, usually associated with something complicated going on at a microscopic scale within the fluid. Some liquids (e.g. milk) are actually an emulsion: droplets of one liquid suspended in another (in milk the suspended droplets are the fat). Others have solids suspended in them– muds, for instance (which can be considered liquids as they do flow) are a suspension of soil particles in an aqueous background liquid. Many synthetic and biological fluids– ranging from shampoo to molten plastics and even saliva– have long polymer molecules moving around within the fluid.
Molten chocolate is another complex fluid. Chocolate is a mixture of cocoa solids, sugar crystals, and fats. At the temperatures found in a running chocolate fountain (around 40° C), the fats have melted but the cocoa solids and the sugar are still in their solid form, giving us a suspension of two different kinds of solid particles. The shape of the sugar particles depends on whether or not the chocolate has been tempered during manufacture, by raising it to a very high temperature and then quickly cooling it. Add to that complexity the strange fact that the behaviour of the cocoa butter depends on the year of harvest, and we have rather an unpredictable non–Newtonian fluid on our hands.

Faced with modelling a fluid this complex, it’s often best to take an engineering approach and simply measure the behaviour of the fluid in a simple flow, rather than trying to predict it. The property we usually try to measure is the fluid’s viscosity or thickness. For a Newtonian fluid at a controlled temperature and pressure, this is a single number– here are a few of them:
Fluid – Viscosity (Pa s)
Water –
Olive oil –
Glycerol –
Liquid honey –
Golden syrup –
Glass –
Viscosities of a range of Newtonian fluids, at a pressure of 1 atmosphere and room temperature, 20.2° C. The SI unit of viscosity is the Pascal second; . Taken from [3].
The viscosity is an essential property of the fluid because it determines how fast energy is dissipated, during flow, by the friction within the fluid. This dissipation balances against the rate at which energy is supplied (by gravity, say, or some forcing like a propeller) to determine how fast the fluid will flow.
The standard way to measure the viscosity of a fluid is to apply a very simple flow called shear flow, which is created by sliding one plate over another with the fluid confined between them:
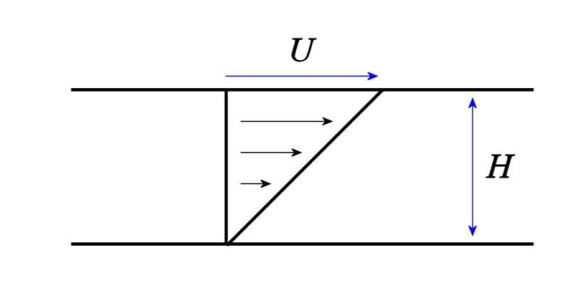
We can measure the force F required to drive the top plate at a given speed U. For a Newtonian fluid, we always find that the force is proportional to the velocity, , and if we name the area of the plates as A and the shear rate
, we can extract the fluid’s viscosity:
.
One of the most common differences between the behaviour of a non–Newtonian fluid and a Newtonian fluid is that viscosity for a non–Newtonian fluid is often not a constant. Instead it depends on how fast the applied shear flow is: specifically, it depends on the shear rate .
Because in more complex flows, the shear rate is likely to be different in different flow regions, this can have a big effect on how the fluid flows. So knowledge of experimental behaviour of a non-Newtonian fluid in shear flow is a vital ingredient in any mathematical modelling of the flow.
Luckily for us (I’m absolutely not an experimental scientist) people have done this with chocolate before. There are many papers available on chocolate rheology [5], all of which attempt to answer our key question
How does the viscosity of chocolate depend on the shear rate?
Of course, because of the differences in composition of different chocolates, and the idiosyncrasy of the harvest, these papers give many different answers to the question. I’ve chosen here one answer (taken from page 11 of [1]) which is my favourite simply because it is mathematically clean:
where the shear rate is measured in reciprocal seconds. As the shear rate increases, the viscosity decreases: so chocolate is a shear-thinning fluid.
What other non-Newtonian fluids are there? The range is wide, but here are a few of my favourites.
Oobleck is a new name for an old thing. If you mix 2 parts cornflour (cornstarch) with 1 part water you get something between a liquid and a solid. It’s not easy to mix it smoothly (if you are actually wanting to use it to make gravy, you would add more water) but once you have, you can pour it as a liquid. But if you stir it too fast it will crack like a solid; and (great for demos) if you punch straight down into a big bowl of it you don’t get wet. If you make enough of it you can run across the surface; but if you stand still you will sink. YouTube is the best place to see it in action [4]. This is a shear–thickening material: when you apply fast flow rates to it, it gets very thick indeed (to the point of behaving like a solid).
Toothpaste is an example of a material with a so–called yield stress. This means that under very light forcing (such as gravity, while it’s sitting on your toothbrush waiting for some action) it doesn’t flow at all. It’s designed like this precisely so it doesn’t run off the brush while you’re putting the lid back on the tube; but once you start brushing (applying a fast shear flow) the paste flows quite easily to distribute around your teeth. It’s an extreme example of a shearthinning fluid (as the viscosity looks almost infinite when there is no flow).
Blood is also shear thinning. At very low flow rates it needs to be thick so that if you’ve been cut, the blood will hang around at the site of the wound long enough for clotting to start; but we need it to be thin while it’s being pumped around the body otherwise the strain on the heart would be too much. Here it’s the deformable blood cells that provide most of the fluid complexity.
Volcanic lava is also shear–thinning; in fact its behaviour (at larger scales, higher temperatures, and larger overall viscosity) is rather similar to that of molten chocolate. In fact this is not so surprising: it has unpredictably shaped rocks suspended in it just as the chocolate has unpredictably shaped sugar crystals.
So now we have a model for the viscosity of chocolate (or indeed lava).
Remember that question at the beginning about the sheets falling inwards? We can answer that without even using any fluid mechanics– or any equations –at all. It’s pure surface tension: water would (and does) do the same thing. Think of a small horizontal section through the falling sheet. The cross–section is an annulus of chocolate. Now look at the surface tension forces acting on an angular segment of that:
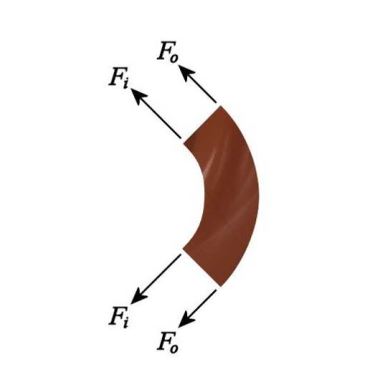
We don’t even have to calculate here! As long as we know that the magnitudes of the two inner forces are equal, and the magnitudes of the two outer forces are equal, we can see that the vector sum of the inner forces will act leftwards and so will the vector sum of the outer forces. So all the surface tension acts to pull this segment to the left, which means this section of chocolate will move leftwards over time. Because we chose a section at the right hand side of the circle that means it will move towards the centre as time passes.
Zoom back out to the 3D sheet of falling chocolate. Each segment moves towards the centre over time. But, of course, each segment is also falling as time passes; so the result is that the radius at the bottom is smaller than at the top. The sheet has been pulled inwards by surface tension.
Article by Helen Wilson
Acknowledgments
This work was originally an MSci project that I supervised; Adam Townsend did all of the work. It is now an Open Access article [2]
Thanks to Girls’ Angle and their magazine the Girls’ Angle Bulletin, Volume 9, Number 6 , where this article originally appeared.
Bibliography and Notes
[1] Melting chocolate. S. Radosasvljevic, A. Schlunk, R. Tanner, and S. Nasseri. Technical report, CRC for Polymers, Sydney, February 2000.
[2] The fluid dynamics of the chocolate fountain. A. K. Townsend and H. J. Wilson. European Journal of Physics 37:105803 (2016).
[3] The Engineering ToolBox.
[4] Biking across a Pool of Cornstarch. Hard Science.
[5] Rheology (not a typo for theology) is the study of the deformation and flow of matter. It’s a growing scientific discipline as we gradually realise that almost everything we process in industry is non–Newtonian.






