Professor Sarah Hart
Gresham Professor of Geometry and Professor of Mathematics at Birkbeck, University of London
This article explores the mathematics of how sounds are made, and what kinds of sounds fit harmoniously together. It is based on a talk which was given as part of a series of public lectures at Gresham College, which has been providing free lectures for over 400 years.
What Is a Sound?
Sounds arise from variations in air pressure. The greater the variation in pressure, the louder the sound. Human ears can detect remarkably small deviations in air pressure, as little as 0.00000002%. Interestingly, it is almost impossible to tell with the naked eye the difference between structured sounds and random noise.
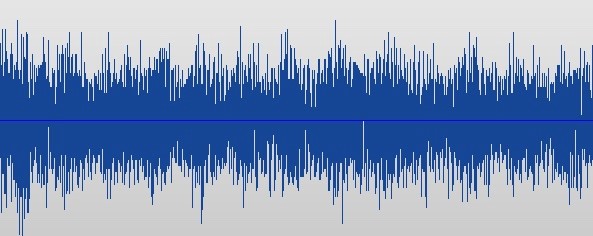
Beethoven’s 5th Symphony
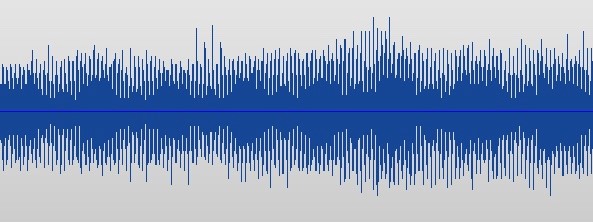
White noise
When we look at the sound made by a musical instrument, we see the same shape repeating. That regularity is what gives it a pitch, making it a note. The frequency with which the pattern repeats determines how low or high the corresponding pitch will be – the higher the frequency, the higher the pitch.
A musical sound wave has four main attributes:
- Amplitude – the size of the vibration: this determines how loud the sound is.
- Frequency – how regularly the vibration repeats: this determines the pitch.
- Spectrum – the shape of the repeating pattern: this determines the quality or timbre of the sound
- Duration – how long the sound lasts.
Frequencies are usually measured in Hertz (Hz), or repetitions per second. A higher frequency is perceived as a higher pitched sound.
Pythagoras and Sound
The study of sound goes back thousands of years. Legend has it that Pythagoras, passing a blacksmith’s shop one day, heard several blacksmiths’ hammers striking their anvils. Sometimes when two hammers struck at the same time, the combined sound would be pleasant, but at other times it would sound horrible. Eventually he realised that when the sounds blended together harmoniously, the hammerheads were related in exact ratios like 2:1 and 3:2. He rushed home to try this out – not with different weights of hammer but with different length strings, on a simple instrument called a monochord.

A monochord like Pythagoras might have used.
Unfortunately, the blacksmith story is probably a myth – doubling the weight of a hammer head does not have the same effect on pitch as doubling the length of a string. But it doesn’t matter: the mathematically important part of the story is the experiments with stringed instruments.
What the Pythagoreans found was that if you pluck a string, and then halve the length and pluck it again, the two sounds produced are very similar, and sound pleasant together. Strings two-thirds or three-quarters as long as the original also make pleasing harmonies with the original string.
From now on we will talk about relative frequencies of these tones, rather than string lengths. Frequency is inversely proportional to string length, so halving the string length results in strings in the ratio 2:1 in length, and has the effect of doubling the frequency. The two other important intervals are obtained from ratios 3:2 (the shorter string is two-thirds the length and the frequency increases by a factor of 3/2) and 4:3 (the shorter string is three-quarters the length, raising the frequency by a factor of 4/3).
The halving of the length of a string produces a sound so similar that we almost think of it as the same note. Nowadays we call the interval between the two notes an octave.
The Mathematics of Frequency
It wasn’t until the 17th century that rules about the frequency produced by vibrating strings were clearly formulated. Vincenzo Galilei had discovered that the pitch of a vibrating string is proportional to the square root of the tension at which it is held – this is a contender for the earliest known discovery of a square root law.
Vincenzo’s son was in fact the famous Galileo Galilei (1564-1642) and he contributed to the theory as well.

Galileo Galilei (1564-1642)
In Galilei’s last book Dialogues Concerning Two New Sciences (1638), there is a long discussion of vibrations and sounds. Galileo says that the frequency of a vibrating string is inversely proportional to its length, directly proportional to the square root of the tension, and inversely proportional to the square root of the string’s weight.
Anyone who has played a guitar or other stringed instrument has experienced the fact that you can, for example, raise the pitch (increase the frequency) either by shortening the string (by pressing your finger against a fret), by tightening the screw on the string to increase the tension, or by using a lower density string.

At almost the same moment, Marin Mersenne (1588-1648) was independently stating essentially the same formulae for vibrating strings. They are now known as Mersenne’s laws.
Nowadays we encapsulate these laws in the following equation:
Here, is the frequency in Hertz (Hz),
is the length of the string (in metres),
is the tension (in Newtons), and
is the linear density (mass per unit length, in kg per metre).
Why Do Different Musical Instruments Sound Different?
When a musical instrument is played, the sound we hear is based on the initial “transient” part of the sound, and then the set of resonant frequencies that make up the main part of the sound. In a stringed instrument, such as a violin, we set one (or more) strings vibrating by either plucking or using a bow to move the string. The transient sound is critical to our experience of it, but very tricky to analyse mathematically. However, the main part of the sound is somewhat easier to analyse.
For instance, in a string fixed at both ends we have something called the wave equation. If we have a string fixed at both ends, and we disturb it in some way at time , then the displacement
of the string at point
after time
is a function of both
and
. The equation it satisfies therefore depends on both
and
. The exact relationship is given by the wave equation, as shown – but feel free to ignore it if you don’t understand the symbols!
Here, is the tension in the string, and
is the linear density. Essentially it is saying that the way in which the displacement
varies as a function of time is very similar to the way in which it varies as a function of the position along the length of the string.
Fourier Series
Now we can use a brilliant bit of mathematics invented by Joseph Fourier (1768-1830). While he was researching the conduction of heat, Fourier managed amazingly to show that any periodic function can be broken up as a combination of sine waves. It’s possible to work out exactly which sine curves are used, and this in turn allows us to replicate sounds electronically.
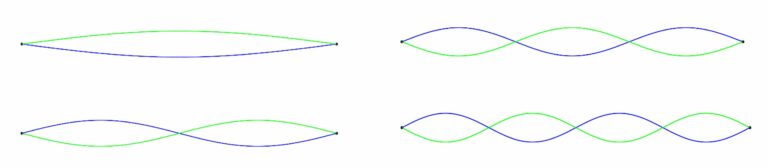
It turns out that each solution to the wave equation for a string fixed at both ends is a linear combination of sine curves of period . The smallest of these would correspond to the function
writing for an arbitrary variable. But we also have
,
,
and so on. The first of these gives a pure sound with frequency, say,
. The second would then have frequency
, and so on.
The way the string is set in motion, along with the shape and size of the instrument, and what it is made of, all play a role in determining the relative amplitudes of the harmonics that make up the sound. It is this which makes different instruments sound different.
The sine wave corresponding to the fundamental frequency (the first harmony) and the subsequent three harmonies, are shown below – we show the highest and lowest positions of the string in blue and green.
By the way, as these harmonics most naturally arise in stringed instruments, in cultures where the instruments are different, our musical scale would not necessarily be the most “natural”. David Benson, in his book on mathematics and music (Benson, D., 2006. Music: A Mathematical Offering. Cambridge: Cambridge University Press), gives the example of the Indonesian Gamelan, where the instruments are all percussion based. Percussion instruments do not produce exact integer multiples of a fundamental frequency, and so the Western musical scale does not work with Gamelan music.
And Finally…a Musical Illusion
Now that we understand how sounds are made up, in theory we can produce any sound by simply adding together the desired component pure tones. This simplifies things slightly if we genuinely want to synthesise a real musical instrument, but if we don’t want our sound to feel artificial, we have to also mimic the transient sound at the beginning of the sound.
It also allows us to play around and create some strange sound illusions, a bit like an audio version of an optical illusion. One of these was invented by the American cognitive scientist Roger Shepard and is a repeating scale that appears to be rising and rising forever.
This is done by creating each tone out of ten harmonics spaced one octave apart, in such a way that the middle ones are loudest, getting quieter at the top and bottom ends, in the same pattern each time. Shepard scales have been used in several pop songs (most recently the Franz Ferdinand track Always Ascending (2018), whose accompanying video was shot in a way that the camera also appeared to be always rising).
What is known as a ‘Shepard glissando’, is a continuous sound rather than a discrete set of tones and was also used in the 2008 Batman film The Dark Knight for the sound of Batman’s motorbike (the Batpod) to give the impression that it was constantly accelerating.
Further Information
The full one hour Gresham Lecture ‘The Sound of Mathematics’ is available here.
A related article on the mathematics of musical composition: https://www.mathscareers.org.uk/the-mathematics-of-musical-composition/
Article by Professor Sarah Hart, Gresham Professor of Geometry and Professor of Mathematics at Birkbeck, University of London

Twitter: @sarahlovesmaths
Images
Featured Image by Pete Linforth from Pixabay
Monochord – Bautsch, CC0, via Wikimedia Commons
Guitar by Louis Hansel on Unsplash