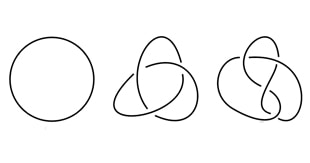Have you ever struggled to untie a particularly tight knot, battled with the jumbled mess of cables hidden behind your PC, or wondered why your shoelaces won’t stay tied? If so, you’re in good company, as mathematicians have wrestled with knots for over 200 years. Knot theory is about more than just tangled pieces of string though, and has applications in biology, chemistry and physics.
All Tied Up
Unlike the knots you use everyday, mathematical knots are joined at the ends, allowing mathematicians to manipulate a knot without accidentally undoing it. The main question in knot theory is whether you can transform one knot into another without cutting it open, but finding the answer is more difficult than it seems.
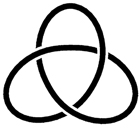 Instead of working with real string, mathematicians draw knot diagrams such as the one pictured left. This knot is called the trefoil knot, due to its three-fold symmetry, and the three points at which the string crosses over itself are represented by breaks in the diagram. The trefoil is the simplest “non-trivial” knot, meaning that it has an interesting feature, but the very simplest knot isn’t actually a knot at all – it’s just a loop of string, called the “unknot”.
Instead of working with real string, mathematicians draw knot diagrams such as the one pictured left. This knot is called the trefoil knot, due to its three-fold symmetry, and the three points at which the string crosses over itself are represented by breaks in the diagram. The trefoil is the simplest “non-trivial” knot, meaning that it has an interesting feature, but the very simplest knot isn’t actually a knot at all – it’s just a loop of string, called the “unknot”.
There are three ways of manipulating a knot diagram, known as the Reidemeister moves. You can twist or untwist a strand, move one strand over another, or move one strand over a point where two others cross. In the 1920s, the German mathematician Kurt Reidemeister proved that if two knot diagrams represent the same knot then you can always transform between them using a sequence of these three moves. Of course, the trick is finding the correct sequence.
Is there a sequence that transforms the trefoil into the unknot? Experimentation suggests that there isn’t, but can we ever be completely sure? Reidemeister moves alone can’t easily prove that two knots are the same, so mathematicians look for properties known as “knot invariants” to help tell them apart.
Knot or Not?
A mathematician presented with a mess of tangled string might stumble across the right combination of Reidemeister moves that transforms it into a recognisable knot, but it’s not possible to tell just by looking at the knot diagram. A knot invariant is a certain quantity defined for every knot that is the same for all equivalent knots, and these can be calculated from a knot diagram.
One simple knot invariant, called tricolourability, asks whether it is possible to colour a knot according to a few simple rules. First divide a knot into strands, the sections of string between each under-crossing. The knot is tricolourable if each strand can be coloured with one of three colours, while also ensuring that at least two colours are used, and that when the strands cross they are either all the same colour or all different colours.
 Following these rules, we can show that the trefoil is tricolourable but the unknot isn’t, because it only requires one colour while the rules state you must use two. Knot invariants aren’t changed by Reidemeister moves (hence the name) so tricolourability proves that there isn’t a sequence of moves to transform the trefoil into the unknot.
Following these rules, we can show that the trefoil is tricolourable but the unknot isn’t, because it only requires one colour while the rules state you must use two. Knot invariants aren’t changed by Reidemeister moves (hence the name) so tricolourability proves that there isn’t a sequence of moves to transform the trefoil into the unknot.
This example shows that tricolourability works, but it isn’t very practical for large and complicated knots, so mathematicians have created other knot invariants such as knot polynomials, which are equations whose coefficients describe the particular properties of a knot. Unfortunately, there is no perfect invariant that can describe all knots individually. Although equivalent knots always have the same invariant, the reverse isn’t true – two knots with the same invariant aren’t necessarily equivalent, meaning it isn’t always possible to tell two knots apart.
Straightening out Science
Unravelling the problems of knot theory and invariants is an ongoing area of research, but it’s more than just mathematical curiosity. Knots are found inside the cells of every living organism, in the form of DNA molecules that contain the genetic instructions needed for reproduction, and biologists use knot theory to understand how DNA unwinds to be replicated. Chemists also use knot theory to study symmetry in other types of molecules, as a knotted molecule can behave differently to its mirror image. Knot theory might even help solve the mysteries of the universe, as physicists have found that knots could bring together the theories of quantum mechanics and general relativity. How’s that for a knotty problem?