Article by Dr Alan Stevens CMath FIMA
Despite being first developed during World War One, Battleships is an iconic game of the 70s and 80s with many treasured copies still hidden away at the back of dusty games cupboards. You might have your own personal theories on how to win – but can mathematics help us beat our opponent? What are the best strategies and is there an easy path to victory?
What is Battleships?
First of all, let’s clarify the rules of Battleships – without this we can’t analyse the strategy. It is a two-player game, where each player has five ships (they are carrier, battleship, destroyer, submarine and patrol boat in the Hasbro version of the game), which they place somewhere on their own 10 x 10 square grid. The ships each occupy a certain number of adjacent grid positions (five for the carrier, four for the battleship, three for the destroyer, three for the submarine and two for the patrol boat) and can be placed only either horizontally or vertically, not diagonally. Figure 1 shows the grid with an example placement of the ships.

Figure 1: A typical Battleships layout.
Each player takes turns to shoot, blindly, at their opponent’s grid by naming a grid reference. The player being shot at calls ‘hit’ or ‘miss’ as appropriate, then takes their turn to ‘shoot’ at their opponent’s grid. (In the standard version of the game, when a ship has had all its grid points hit, the player states what ship has been ‘sunk’; however, the instructions also allow for the harder version in which this is not required. Only the latter, harder version is considered here.)
In the peg-board version of the game, both players insert a white peg for a miss or a red peg for a hit in a hole at the appropriate grid point (the player taking the shot has a blank grid to record their successes and failures). The first player to hit all the grid points occupied by ships is deemed to have destroyed their opponent’s fleet and hence wins the game. There are several variants of the procedure, but this simple one is all we will consider here.
Three Different Strategies
Let’s compare three different shooting strategies, from mindless to more thoughtful, to see how many shots it might take, on average, to destroy our opponent’s fleet.
Totally Random Strategy
We will start with the totally random approach, in which we just shoot randomly all over the grid, irrespective of what we hit or miss (though we will keep track of where we shoot, and will avoid shooting at the same grid point twice). We will assume our opponent has the ship placements as shown in Figure 2.

Figure 2: Sample battleship grid used in these simulations
We will play games of mindlessly blasting away, aiming at the grid points in a different random order each time. A histogram of the number of shots it takes to sink the fleet of Figure 2 is shown in Figure 3. What we have done here is perform a Monte-Carlo simulation which a really common technique used in the real world. In a Monte-Carlo simulation computers run different scenarios thousands of times to find out information on the probability of different outcomes. No human would ever have time to sit down and play
games of Battleships, so the computer does the work for us.
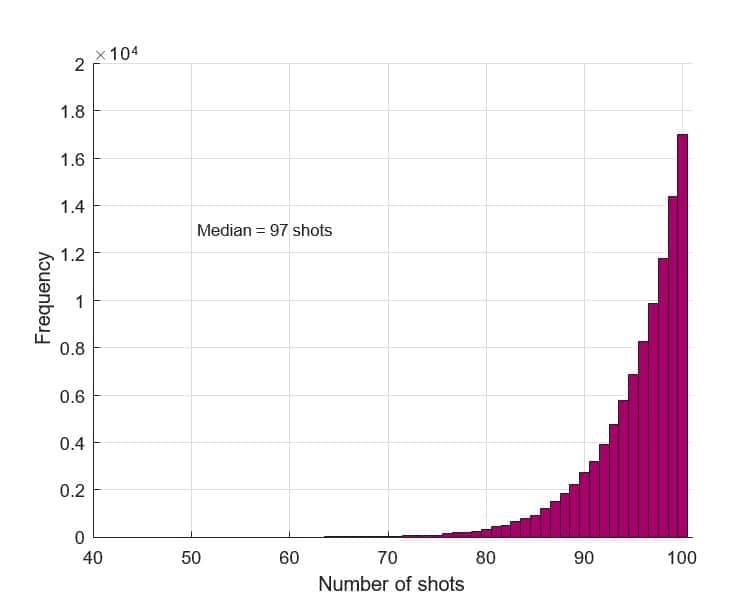
Figure 3: Fleet Destruction using the Totally Random Strategy
Since there are 17 grid points occupied by a fleet, the minimum possible number of shots to destroy it is 17. The probability of doing that with this totally random approach is almost zero! The maximum possible number of shots is 100, and it is clear from Figure 2 that this does happen! Using this strategy it takes a median 97 shots to sink the opponent’s fleet showing that it is a terrible strategy.
Search on Hit Strategy
Of course, we can generally do much better than this by recognising that each time we hit a ship, there will be another part of the ship to the north, south, east or west of that grid point. So for our second method (search on hit), we will start shooting randomly all over the place, but as soon as we hit a ship, we will shoot at the (up to) four adjacent compass points, as long as we have not already shot at them. Again we will play games against the arrangement of Figure 2. The histograms of numbers of shots to sink the fleets for these first two methods are compared in Figure 4.
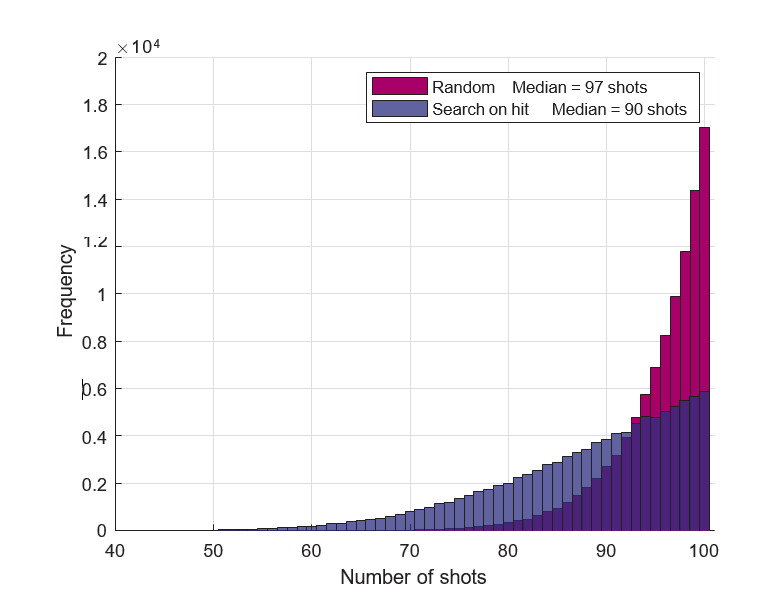
Figure 4: Fleet destruction histograms for the Totally Random and Search on Hit strategies
We can see that there is now a greater chance of sinking our opponent’s fleet in fewer shots than is the case for the random approach. However, on average it still takes 90 shots. Can we do better?
The Chequerboard Strategy

We certainly can do better if we picture the battle grid as having a chequerboard pattern with alternating white and black squares. Since the ships can be placed only horizontally or vertically, every two adjacent squares inside a ship will lie on different colours, one on black and one on white. That means we can improve our hit rate by aiming the random shots at only one ‘colour’ (black or white), then doing the compass point shooting (which will target the other colour) when we get a hit. Yet again, we play games to see how much improvement this strategy brings us. Figure 5 compares histograms of the number of shots to destroy the fleet of Figure 2 for the three strategies.
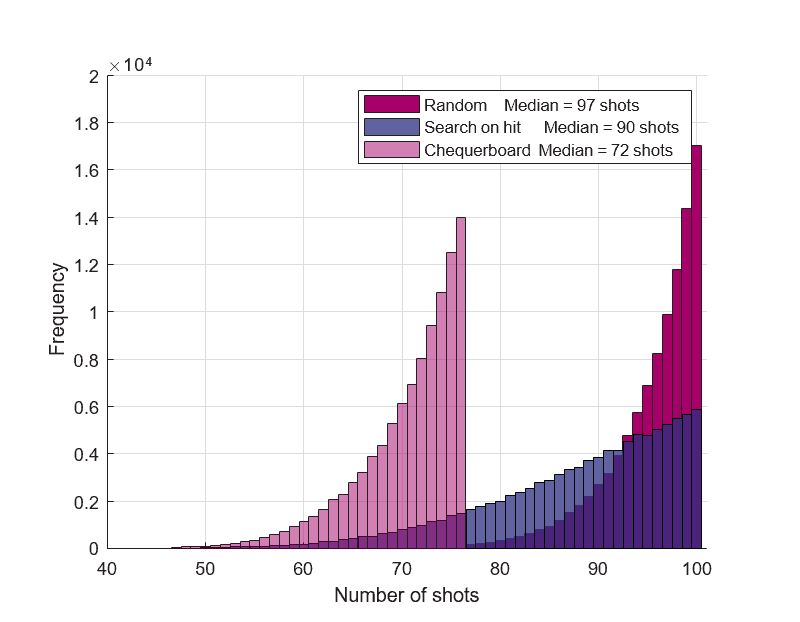
Figure 5: Fleet destruction histograms for the three strategies
There is clearly a significant improvement using the chequerboard strategy, with the average number of shots required now reduced to 72. These three strategies have just been tested here against the arrangement of the fleet shown in Figure 2. Strictly, we should test them against lots of other arrangements. If we were to do this we would find that, although the fine detail might change from one arrangement to another, the overall trend would be similar.
There are other, more complicated strategies one might consider, such as shooting further in a particular compass direction, which in fact is a strategy which is naturally used by human players. I will leave those for you to investigate.
A longer version of this article first appeared in the December 2020 edition of Mathematics Today, the membership magazine of the Institute of Mathematics and its Applications
Featured Image “You sunk my battleship!” (CC BY 2.0) by derekGavey