Look at the world around you. Look closer. Closer still. .. Most everyday objects look very different when you zoom in close. But there are also natural forms that show the same shapes at different scales. This is called self-similarity.
Natural forms are not exactly the same when shrunk down, as nature isn’t great at exact copies. But there are mathematical shapes that have self-similarity. They are called fractals, and they have many other interesting properties.
These shapes can be formed by iteration. This is a process where you change a shape based on a set of instructions. Then the same instructions are applied to the newly changed shape, making it different again. Each time the instructions are repeated is called an iteration. Doing the same thing again and again sounds simple, but it can produce beautiful, complicated results.
A beautiful and unique snowflake
An example of one of these shapes is the Koch Snowflake. Here are the instructions for making it. The following image shows the stages in pictures.
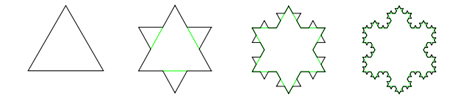
- Start with an equilateral triangle.
- Remove the central third of each line and replace it with two lines of equal length to the one that was removed.
- Now remove the central third of each of these lines and put two lines of equal length to it instead. (This step can be repeated hundreds of times, but each time the line segments being removed are smaller. Very quickly it is hard to see the small changes being made, so there’s no need to repeat it too many times to make this beautiful shape.)
You can see the self similarity in this shape. Zooming in on any of these points shows you see the same shape again and again, just like in the fern. Not only is it beautiful to your eyes, it’s also filled with mathematical beauty. With each iteration, an extra 1/3 is added to each edge, so the whole perimeter gets 1/3 longer.
|
Iteration |
Perimeter length |
|
0 |
L |
|
1 |
L + 1/3L = 4/3L |
|
2 |
4/3L + 1/3 (4/3) L = 4/3L + 4/9L = |
|
3 |
16/9L + 1/3 (16/9)L = (4/3)3 L |
|
n |
(4/3)n L |
This is a diverging sequence – it just keeps getting bigger with each iteration. In fact, if you do the operation an infinite number of times to make the mathematically perfect shape that Helge von Koch described, the perimeter just keeps growing. You end up with a shape with an infinite perimeter! But hang on, what’s happening to the area? It’s certainly not getting 1/3 bigger every time.
|
Iteration no |
Area of triangles added |
Number of triangles added |
Area of triangles |
New area |
|
0 |
– |
– | – |
81 |
|
1 |
9 = a/9 |
3 |
27 |
108 |
|
2 |
1 = a/92 |
12 |
12 |
120 |
|
3 |
1/9 = a/93 |
48 |
5.33 |
125.33 |
|
n |
a/9n |
Comparing the different generations of snowflake, you can see that each iteration adds more triangles to the edges, but these are smaller than the previous ones. Eventually the new triangles shrink to nothing, and it stabilises at a certain value. This is a converging sequence and the value it converges on is finite. We’ve got a finite area enclosed by an infinite perimeter! Surely something’s gone wrong?
Monstrous creatures
 At the start of the 20th century many mathematicians thought that these constructions were deeply, deeply wrong. They even referred to them as ‘monster curves’ because they found them so disturbing.
At the start of the 20th century many mathematicians thought that these constructions were deeply, deeply wrong. They even referred to them as ‘monster curves’ because they found them so disturbing.
They remained something to be swept under the carpet and politely ignored until the 1960s, when a mathematician called Benoit Mandelbrot started studying them. He showed that these shapes, which he named fractals, appeared everywhere. Not only are they good descriptions of many natural surfaces such as trees, veins and the surface of animal lungs, they also turn up when graphing chaos. Here they help in studying wind flow around racing cars, the orbits of the planets, and the movements of subatomic particles, among many others. Not bad for a monstrosity.






