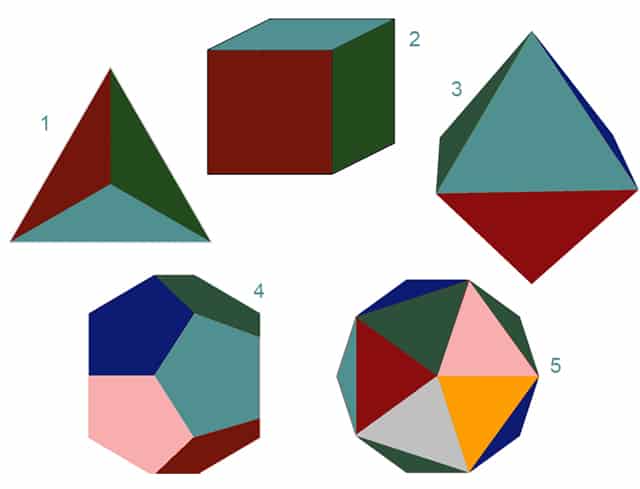
Shapes have fascinated people since ancient times and there is one special group of 3D shapes which has always attracted special attention. The platonic solids consist of five different 3D shapes which satisfy a number of different properties.
Platonic solids must:
- Have the same number of faces meeting at every vertex (corner)
- Each face must be the same regular polygon
Under these rules there are only 5 different possible shapes, shown in the picture below. Can you name them all?
The platonic solids were named after the Greek philosopher Plato. In ancient times some people believed that the whole universe was composed of these special solids. They thought that the earth was made of cubes, the air made of octahedrons, water of icosahedrons, fire of tetrahedrons and that dodecahedrons played a special role in arranging the stars.
You may wonder why there can only be five possible shapes in this special family. There is an easy proof using simple geometry.
1. First of all we know that at every vertex (corner), at least 3 faces must meet. (Otherwise it wouldn’t be a vertex on a 3D shape!)
2. The internal angles at any vertex (corner) must add up to less than 360°. Otherwise the shapes would start to overlap.
3. We can then start looking at regular polygons to see which shapes would work. First of all we will look at equilateral triangles.
| Regular Polygon | Internal Angle | Number of faces meeting at every vertex (corner) | Total angle round each vertex (corner) | 3D Shape |
| Triangle | 60° | 3 | 3 × 60° = 180° | Tetrahedron |
| Triangle | 60° | 4 | 4 × 60° = 240° | Octahedron |
| Triangle | 60° | 5 | 5 × 60° = 300° | Icosahedron |
| Triangle | 60° | 6 | 6 × 60° = 360° | Not possible (too big) |
Next we will look at squares:
| Regular Polygon | Internal Angle | Number of faces meeting at every vertex (corner) | Total angle round each vertex (corner) | 3D Shape |
| Square | 90° | 3 | 3×90°=270° | Cube |
| Square | 90° | 4 | 4×90°=360° | Not possible (too big) |
And next at pentagons:
| Regular Polygon | Internal Angle | Number of faces meeting at every vertex (corner) | Total angle round each vertex (corner) | 3D Shape |
| Pentagon | 108° | 3 | 3×108°=324° | Dodecahedron |
| Pentagon | 108° | 4 | 4×108°=432° | Not possible (too big) |
The next regular shape which is bigger than a pentagon is the hexagon with six sides. A hexagon has an internal angle of 120°. There cannot be a platonic solid made up of hexagons – even if three hexagons meet at a vertex this will create an angle of which is too big.
We have therefore shown that there are only five possible platonic solids. Any others are not possible because the internal angles are too big.
Platonic solids are still studied today, as they feature in many different natural structures. For example many viruses are shaped like icosahedrons and lot of different crystals are also made up of platonic solids. In 2011 Dan Shechtman discovered an icosahedral form of aluminium which earned him the Nobel prize for chemistry.
Mathematical ProofOne of the most important features of mathematics is that ideas can be proved, meaning that we can show something is definitely true (or not true). In the case of platonic solids we have not only found the five platonic solids, we have also shown that there cannot be any more. This is often a major difference between mathematics and science. In science evidence is used to show that an idea is almost certainly true, whereas in mathematics proof can show that an idea is true without any doubt at all. |
Article by Hazel Lewis