To apply mathematics to the real world, mathematicians must work with scientists and engineers, to turn real life problems into mathematics, and then to solve the resulting equations. We call this process mathematical modelling. This article will explain the basic ideas behind mathematical modelling, and will try to describe its power and its limitations.
The Basic Ideas Behind Mathematical Modelling
Mathematical modelling is the process of describing a real world problem in mathematical terms, usually in the form of equations, and then using these equations both to help understand the original problem, and also to discover new features about the problem. Modelling both lies at the heart of much of our understanding of the world, and it allows engineers to design the technology of the future. With modelling we can travel to the edge of the universe, peer into the heart of the atom, and understand the future of our climate.
We are all very familiar with one application of mathematical modelling, namely the weather forecast. A modern weather forecast is based on the following steps
- Start with the laws of physics
- Encode these as (differential) equations, in particular the Navier-Stokes equations.
- Take data from satellites and weather stations to determine today’s weather accurately.
- Using this as an initial condition, (using a super computer) solve the equations for 24 hours to give us the weather tomorrow.
- Continuously update the forecast.
- Present the results in a way that all can understand.
 Despite rumours to the contrary this process works, and works well. At least for short term weather forecasting. This process is a special case of the more general process of mathematical modelling which can be described simply as:
Despite rumours to the contrary this process works, and works well. At least for short term weather forecasting. This process is a special case of the more general process of mathematical modelling which can be described simply as:
- Identify the problem i.e talk to the people involved.
- Clarify the science.
- Formulate the science mathematically.
- Solve the mathematics possibly using a computer.
- Draw conclusions.
- Explain your results.
As well as weather forecasting, this process is used to design aeroplanes and cars, develop new drugs, control the electricity supply network and even help establish the cause of the 1987 Kings Cross Fire.
Constructing a Simulation
Strictly speaking what we have described above is a simulation. The difference between a simulation and a model is that in a simulation we are concerned to try to get all of the details as right as possible so that the conclusions are as accurate as possible. Using such simulations we can, for example, determine in advance whether a bridge will stay up after it has been built. We can also test the bridge to destruction without ever having to build it in the first place simply by varying the parameters in the computer simulation. Another important use of simulation is in the training of pilots in aircraft simulators, which are designed to be as close to reality as possible. Using these, a pilot can be trained to fly an aircraft and to deal with dangerous situations, long before they have to enter the cockpit. One of my favourite examples of a simulator is the computer programme used by the line managers to control the operations of the London Underground. Simulators are also used at the heart of many video games. Two examples of such, shown below, are simulators of the underground and of a factory.
 Whilst simulators are very useful, they have big disadvantages. The need for high accuracy means that the equations are usually far too hard to solve analytically. Instead, they must often be solved by using large super-computers. The bigger the computer the better. These simulations often take a long time, consume a lot of energy, and produce vast amounts of data. So much data in fact that it is often hard to work out what is important and what is irrelevant. Furthermore it is hard to use the simulations to do ‘what if’ experiments as they take so long to run and are expensive.
Whilst simulators are very useful, they have big disadvantages. The need for high accuracy means that the equations are usually far too hard to solve analytically. Instead, they must often be solved by using large super-computers. The bigger the computer the better. These simulations often take a long time, consume a lot of energy, and produce vast amounts of data. So much data in fact that it is often hard to work out what is important and what is irrelevant. Furthermore it is hard to use the simulations to do ‘what if’ experiments as they take so long to run and are expensive.
A second disadvantage is that they only tend to work, and be applied to, problems where the basic science is well understood. One reason for this is that it is a very significant amount of work (in person hours) to write and code a simulator. You do not want to put such an investment into a system which you do not understand well.
The Process of Mathematical Modelling
We contrast simulation with a mathematical model. This is a simplification of the problem to a small system of equations, which capture the essential essence of it, and, crucially, are simple enough to allow us to make analytical calculations. A formula derived from an analytical calculation can give a clear view of the role of the parameters in that system without having to run a very large number of calculations.
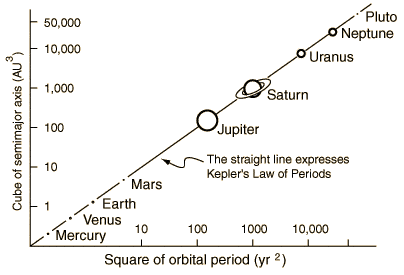
Perhaps the earliest example of a mathematical model of enormous predictive powers was Newton’s law of gravitation applied to the solar system. Rather than modelling the whole system in all of its complexity, he treated the Sun and the planets as single points. This allowed him to write down the basic equations of motion of the whole of the solar system.
 The process of simplification in constructing a model is hugely important, but also hard. A wonderful quote from Albert Einstein is:
The process of simplification in constructing a model is hugely important, but also hard. A wonderful quote from Albert Einstein is:
A model should be as simple as possible, and no simpler
The ‘traditional’, and often taught, approach to constructing a mathematical model is as follows:
- Think about the problem in a mathematical way identifying all of the key ingredients
- Write down the relevant equations, simplifying as much as possible
- Solve the equations
- Compare the results against data
- If the results agree STOP
- If not then modify the equations, such as making them more complex and including new processes
- Repeat from 2 above.
This method of modelling is often taught in universities and at schools. However, there is one problem with this description of the modelling process. In general it is completely wrong. The reason that it is wrong is that it is very, very, rare to come anywhere close to writing down the right equations the first time. Indeed without looking hard at the data to start with, it is likely that the equations will not be anywhere close to the truth. The result is ‘mathematical models’ that might look nice are so far from the truth as to be practically useless. They are also often so simplified, that they also have no real mathematical interest either. In contrast true mathematical modelling plays close attention to the data at all stages of the process, employs computation at all times, and NEVER stops at line 5 above. A mathematical model is a living process, that if looked after well will continue to give insights into the system. Another problem with this approach is that point 4 is often very difficult. What does ‘agreeing with data’ really mean when it comes to a model of (say) loneliness. The best models are ones which give us excellent insight into the system which allow us to make useful future predictions. Quantitative agreement with actual data is often a bonus. Or to quote George Box [1]
All models are wrong, but some of them are useful.
In practice the modelling process (at least in my own experience of over 30 years of solving industrial problems using mathematics) is much more like the picture below:
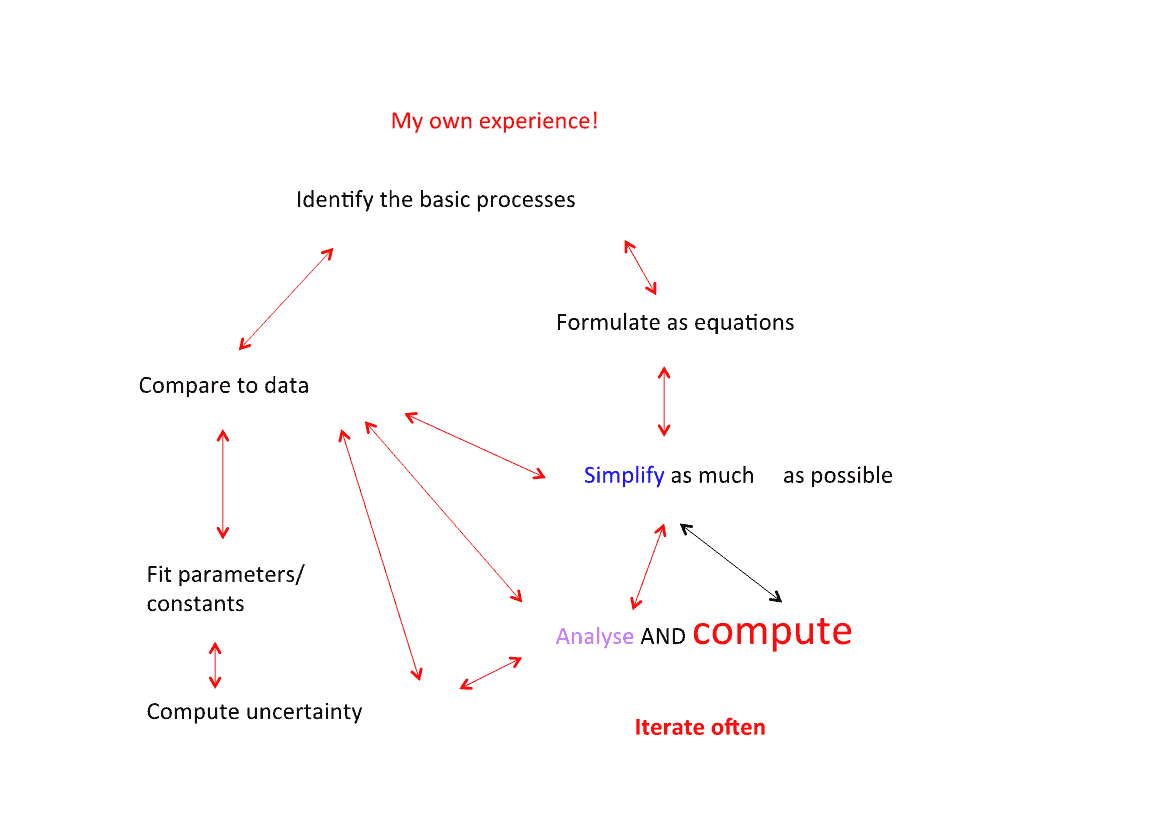 You will probably get the impression from the above that modelling is more of an art than a science. In this you would not be far wrong.
You will probably get the impression from the above that modelling is more of an art than a science. In this you would not be far wrong.
Further Material
Full 58 minute Gresham Lecture on YouTube – Can Maths Save The Whales and Cure Cancer? By Chris Budd
Article by Professor Chris Budd OBE, University of Bath
References
[1] G. Box, ‘All models are wrong but some are useful’, (1976)A discussion of this comment is given in
https://en.wikipedia.org/wiki/All_models_are_wrong
Image credit: https://en.wikipedia.org/wiki/File:Airplane_vortex_edit.jpg by NASA Langley Research Center (NASA-LaRC) / Wikimedia Commons / Public domain






