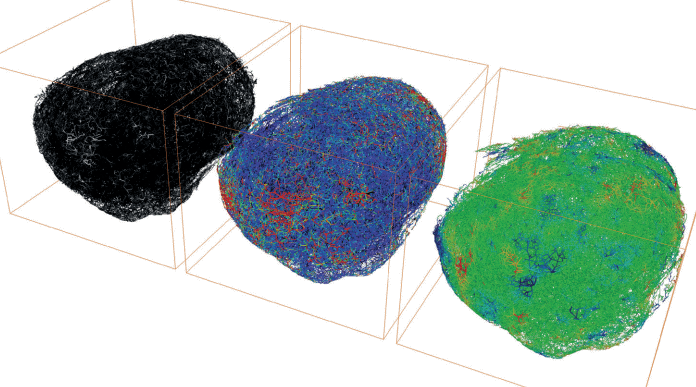Saving Lives With the Help of Mathematics
One in two people in the UK will be diagnosed with cancer in their lifetime. Consequently, cancer treatment costs the NHS many billions of pounds, and so there is an urgent need to develop novel and effective therapies to cope with these demands. One of the challenges is that every cancerous tumour is unique in structure, meaning that it is incredibly difficult to predict whether an anti-cancer drug will be effective.
Tumours contain a network of interconnected blood vessels which transport nutrients, facilitate tumour growth and can be used to deliver drugs. However, due to their complex architectures, the flow of blood is typically much higher near the surface of the tumour, and reduced nearer the tumour centre. This can cause significant resistance to treatment, as there is no guarantee that a drug can be transported throughout the tumour at a high enough dose.
A team of mathematicians and scientists from UCL have been working to overcome this challenge by using advanced biomedical imaging techniques to create detailed 3D virtual tumours which enable them to simulate how a cancer drug will be delivered in a particular tumour.
The researchers treat the blood vessels as a network of interconnected pipes, and apply what is known as Poiseuille’s law to model the flow of blood within these pipes.
Poiseuille’s Law: : flow rate;
: diameter of the pipe;
: blood viscosity;
: length of pipe;
; pressure difference between the start and end of the pipe.
This equation allows the researchers to predict how blood flows within the tumour, to assess how much cancer drug will reach each part of the tumour. Initially this research will be used in preclinical testing of new cancer drugs and treatment strategies on a wide range of cancer types. However, in the future it is hoped that this research will enable patients to receive a much more personalised dosage of therapy, tailored to individual tumours, reducing side effects and making treatment more effective.
Article by Hazel Lewis