Modelling Tumour Growth
Cancer is the name given to diseases which are characterised by rapid, uncontrolled cell growth. There are over 200 different types of cancer, classified by the type of cell that is initially affected. Normally, our bodies form new cells only as we need them. However, when cells acquire mutations that disrupt the tightly controlled processes of cell division and death, a tumour can grow. Mathematical models allow us to quickly search and identify the most effective drug combinations for cancer patients. They are also deepening our understanding of how and why cancer cells often become resistant to chemotherapy drugs. Mathematical and computational modelling approaches, usually based on differential equation models, have been applied to every aspect of tumour growth. An excellent summary of these is given in [1].
For example, a differential equation for the rate of growth of a tumour of density c is given by:
Here the first term on the right-hand side of this equation describes the dispersal of the cancer cells and is similar to the conduction of heat. The second term describes the net proliferation rate, with K being the maximum carrying capacity of the tissue for the cells. Solving this nonlinear equation allows us to estimate how rapidly the tumour will grow in its initial stages of development
Ultimately, the outcomes of all cancers in a patient are a product of tumour biology and the response to therapy. It is really hard for researchers to investigate these different factors in real patients, however mathematicians have created a virtual tumour by using a mathematical model. This provides a way of investigating the relationship between biology and the outcomes of treatment. Such models should then be used to inform and guide a spectrum of clinical trials to improve outcomes for patients suffering from cancer. To quote [1] ‘the field of mathematical oncology has the opportunity to drive forward a completely new trajectory of precision treatment strategies for cancer patients’.
Destroying Tumours by Sound
In another article we look at how it is possible to use maths to locate a whale by listening to both the sound it makes and also the echoes of that sound. In this section I will take the maths in the opposite direction, and will describe a procedure I have been involved with that uses the same ideas to help cure cancer. When looking for the whales we were keen not to use sonar in case it damaged the whale. However, in treating cancer we want to be able to damage, indeed to destroy, a tumour, without damaging the surrounding tissues. One way to do this is to generate high intensity ultrasound (very high frequency sound of frequency around 1 MHz) in a transducer. This can then be focused on a tumour in much the same way that a magnifying glass can focus light onto a spot. As we all know from having done this (admit it) the point at the focus then starts to burn.
Exactly the same happens to the tumour, which is then destroyed. If the point of focus is not on the tumour itself, then this process could cause damage to a vital organ. To avoid this, the patient is monitored throughout using magnetic resonance imaging (MRI), which can detect the changes in temperature inside the body. The whole treatment process is called MR-HIFU (Magnetic resonance High Intensity Focused Ultra Sound), and is shown below. The patient lies on top of a table in which there is a transducer producing the ultrasound. They are then surrounded by a large ring, which contains the magnets for the MRI scan.
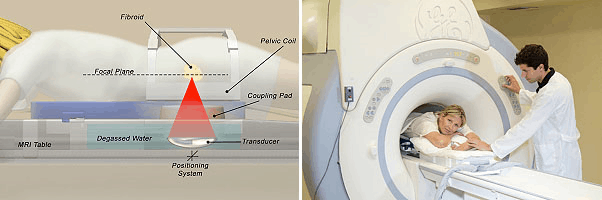Mathematics is needed to make all stages of this treatment work. It is used to design the shape of the transducer, to determine the strength of the sound waves and the time needed for them to radiate the tumour, and to create the images in the MRI scan. This is all done by using mathematical models, and I am pleased to say my introduction to this problem came from a mathematical study group held in Toronto, Canada.
As usual in the mathematical modelling process we start with a picture. Sounds starts from a transducer, travels through layers of the body, and eventually reaches the tumour. The sounds waves are in general of low intensity (they need to be to avoid damaging the body).
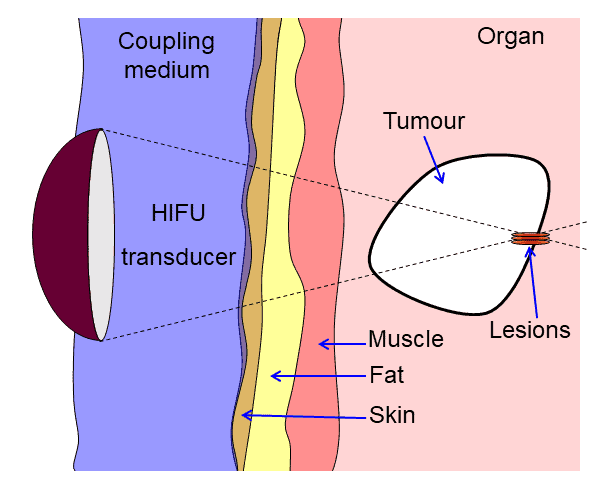The sound waves satisfy the same wave equation as the sounds from a whale, and a simple modelling approximation can then be used both to design the shape of the transducer and to work out approximately where the point of focus will be. (It is never quite exact due to variations in the speed of sound as it travels through different parts of the body.
The result is a method which can be used to destroy tumours safely and reliably. It is still under testing, but has already shown success in destroying tumours in bone cancers at the SickKids hospital in Toronto [2].
What Next?
Given that so much of the real world can be modelled using mathematics, the potential applications of mathematical modelling are almost limitless. Watch this space. But always be aware of the limitations of any model.
References
[1] T. Jackson, N. Komarova and K. Swanson, Mathematical Oncology: Using Mathematics to Enable Cancer Discoveries, (2014), The American Mathematical Monthly, 121:9, pp. 840-856 [2] An account of the uses of the MR-HIFU procedure at the SickKids hospital in Toronto is given in: http://www.sickkids.ca/AboutSickKids/Newsroom/Past-News/2014/SickKids-doctors-destroy-bone-tumour-using-incisionless-surgery.htmlFurther Material
Full 58 minute Gresham Lecture on YouTube – Can Maths Save The Whales and Cure Cancer? By Professor Chris Budd
By Professor Chris Budd OBE, University of Bath
Featured Image Image by by Colin Behrens from Pixabay
Photo by National Cancer Institute on Unsplash
